问题标签 [rotational-matrices]

我在 OpenGL 中遇到问题，让我的对象（行星）相对于当前相机旋转进行旋转。一开始它似乎可以工作，但是在旋转一点之后，旋转不再正确/相对于相机。

我正在计算屏幕上 mouseX 和 mouseY 移动的增量（差异）。旋转存储在名为“planetRotation”的 Vector3D 中。

这是我计算相对于planetRotation的旋转的代码：

理论上 - 这样做是在“rotateAmount”变量中设置旋转。然后通过将此向量与逆模型变换矩阵 (rotMatrix) 相乘，将其放入模型空间。

然后将此转换后的旋转添加到当前旋转中。

要渲染这是正在设置的转换：

相机有点摆动，我试图执行的旋转，似乎与当前的变换无关。

我究竟做错了什么？

我是一名物理学家，并且一直在学习一些编程，并且遇到过很多人使用四元数进行旋转而不是以矩阵/向量形式编写东西。

在物理学中，我们不使用四元数有很好的理由（尽管偶尔会讲述关于汉密尔顿/吉布斯等的离奇故事）。物理学要求我们的描述具有良好的分析行为（这具有精确定义的含义，但在某些相当技术性的方面，远远超出了普通入门课程中所教的内容，因此我不会详细介绍）。事实证明，四元数没有这种好的行为，所以它们没有用，而向量/矩阵有，所以我们使用它们。

然而，仅限于刚性旋转和不使用任何解析结构的描述，3D 旋转可以等效地描述任何一种方式（或其他几种方式）。

通常，我们只需要一个点 X = (x, y, z) 到一个新点 X' = (x', y', z') 的映射，并受到 X ² = X' ²的约束。有很多事情可以做到这一点。

天真的方法是只绘制这个定义的三角形并使用三角学，或者使用点 (x, y, z) 和向量 (x, y, z) 之间的同构以及函数 f(X) = X' 和矩阵 MX = X'，或使用四元数，或使用其他方法将旧向量的分量沿新向量投影出 (x, y, z) ^T .(a,b,c) (x',y', z') 等。

从数学的角度来看，这些描述在这个设置中都是等价的（作为一个定理）。它们都具有相同数量的自由度、相同数量的约束等。

那么为什么四元数似乎比向量更受欢迎呢？

我看到的通常原因是没有万向节锁或数字问题。

没有万向节锁的说法似乎很奇怪，因为这只是欧拉角的问题。它也只是一个坐标问题（就像极坐标中 r=0 处的奇点（雅可比失去秩）），这意味着它只是一个局部问题，可以通过切换坐标，旋转出简并来解决，或使用两个重叠的坐标系。

我对数字问题不太确定，因为我不详细了解这两个（以及任何替代方案）将如何实现。我读过重新归一化四元数比对旋转矩阵进行归一化更容易，但这仅适用于一般矩阵；旋转有额外的约束，使其变得微不足道（这些约束内置在四元数的定义中）（事实上，这必须是真的，因为它们具有相同数量的自由度）。

那么在向量或其他替代方案上使用四元数的原因是什么？

不久前我在推特上发布了这个，但看到我的追随者似乎都不是数学/编程天才，我也会在这里试试运气。我来到这里是因为我发现这可能包含我的解决方案的一部分。

我在以下pdf文档中描述了我的问题，其中包含我想要实现的目标的图片。

为了提供更多细节，我将十二面体的五边形（12 个五边形）划分为三角形（5 个/五边形，总共 60 个三角形），然后收集与每个三角形相关的一组数据点。

这个想法是为每个单独的三角形生成地形网格。为此，数据必须以 32K x 32K 正方形（idTech4 Megatexture）平面表示

我隐约听说过转换矩阵，如果设置得当，它可以起到将所有数据点通过它们的技巧，让它们出现在正确的位置。

我在这里查看了这个源代码，但我不明白我应该如何将点输入和/或输出，更不用说如何进行设置，以便我可以依次呈现每个点并获得结果点回来。

我很快就确定了属于右后角的点。我所有的 3D 点最初都存储在纬度/经度对中。我以这种方式检索 3D 向量：

我的想法是，如果我能找到我的三角形的中心，并发现如何偏移我的角度，以便从我的球体中心到三角形中间的矢量移动到 90N，那么我的点将已经在正确的平面上，如果我沿相同的角度旋转它们。如果我然后将它们全部转换为 3d 并从 y 中减去半径，它们也将位于正确的 y 位置。

然后我需要做的就是旋转、缩放和移动到最终位置。

三角形有几种“中心”，我认为我需要的是与三角形角等距的一种（外心？）

但是可能有一个更简单的方法来解决整个问题，所以当我继续我自己的研究时，也许你们中的一些人可以帮助我指出正确的方向。

看起来好像一些样本数据是有序的，这里有一些 obj 文件格式的三角形：

还有一个：

您会注意到，每个点与 0,0,0 的距离为 3396 我提到“在球体上”，这意味着远离球体中心的面是在翻译成时需要成为“顶部”的面广场。

从理论上讲，所有这些三角形实际上应该具有相同的大小，但是由于生成它们的数学中的舍入误差，这可能并不完全正确。

如果我没记错的话，我已经采取措施确保您在这里看到的第一个点始终是与最长边界相对的那个点，所以它应该位于最左角（测试上述 2 个样本证实了这一点，但是无论如何，我正在测量以确保）从这一点引出的两条腿理论上也应该具有相同的长度，但再次舍入误差可能会稍微抵消这一点。

如果我做得正确，那么长边是 2 个短边的 1,113587 倍。假设它们是相同的，然后在 excel 中进行一些目标搜索，我可以推断出最终点，假设我只是在翻译这个三角形，应该如下所示：

所以我需要设置矩阵来进行这种转换，最好使用 4x4 矩阵，如下所述。

我正在尝试恢复图像中建筑物三个轴的 3D 方向。

我目前的做法是手动标注三个轴对应的三个消失点，估计相机标定矩阵K，然后通过归一化K^{-1}v_{i}从一个消失点计算旋转矩阵的每一列，如本文附录中所述。

尽管这似乎可行，但 R 的计算列并不完全正交，我怀疑如果消失点更嘈杂，问题会更加明显。

我可以通过使用 SVD 分解估计的 R 并将所有奇异值设置为 1 来捏造它，但我更喜欢更有原则的解决方案。另一种思路是将其作为一个约束优化问题来解决，该问题旨在最小化消失点上的投影误差。

有没有更好的方法从 K 和消失点计算旋转矩阵，同时考虑正交性和列统一约束？

提前致谢。

我创建了一个画布并在其上绘制了位图，并在每次触摸画布时对其进行动画处理

我已经在绘图开始时设置了位图的边界，但是在我更改旋转矩阵并旋转位图之后，它不会根据新矩阵更改边界

我需要重置位图的边界才能将其用作可点击对象并在点击它时触发一些事件

如何根据旋转矩阵更新边界

提前致谢

我正在尝试对速度计进行编程，以便稍后用 GPS 数据或其他东西填充它。我有一个 ImageView，它显示针（480x480）作为源，速度计作为背景图像（480x480）。现在我尝试使用以下代码旋转指针：（一个单位 [km/h] 是 2.25° 的角度）

目前效果很好。但是当针转动时，布局的大小就会妥协。我猜这是因为图片的对角线大于高度，并且在转动矩阵时，布局会延伸到其全高（那时就是对角线）。所以我的车速表总是在变化。有什么想法我能做什么？

我遇到的问题是，我需要从 XYZ 固定轴旋转转换为围绕 Z 的欧拉旋转，然后是 X'，然后是 Z''。

以下是相关矩阵：

X：

是的：

Z：

组合起来，如 Rz(psi) Ry(phi) Rx(theta) = Rxyz(theta,phi,psi)；他们给：

回复：

以及我想要的欧拉角特定约定的旋转矩阵；这是：

欧拉：

所以我最初的计划是比较矩阵元素，然后提取我想要的角度；我想出了这个（最后的实际当前代码）：

但这在几种情况下不起作用。最明显的是当 Cos(theta)Cos(phi) == 1; 从那时起 Cos(beta) = 1，因此 Sinβ = 0。其中 Sin(beta) 在代码中是 s2。这仅在 Cos(theta) 和 cos(phi) = +/- 1 时发生。

所以我马上就可以排除可能的情况；

当 theta 或 phi = 0, 180, 360, 540, ... 时，则 Cos(theta) 和 Cos(phi) 为 +/- 1；

所以我只需要对这些情况做不同的处理；

我最终得到了这段代码：

其中 r 和 eq 只是两个简单的函数；

eq 只是为了比较测试的数字，而 r 是为了防止浮点错误将数字推到 Math.acos / Math.asin 范围之外并给我 NaN 结果；

（即时不时地我会以 Math.acos(1.000000000000000004) 或其他东西结束。）

其中考虑了围绕 x 和 y 旋转的 4 种情况，这些情况使 c2==1。

但现在是问题发生的地方；

我在上面所做的一切对我来说都很有意义，但它没有给出正确的角度；

这是一些输出，在每一对中，第一个是 theta phi psi 角度，每对中的第二个是相应的 alpha beta gamma 线。忽略舍入误差，似乎有些角度偏离了大约

我认为这是由于 Math.acos 和 Math.asin 的工作方式，有人能想到解决方案吗？

编辑： math.asin 和 math.acos 分别返回 -pi/2 和 pi/2 以及 0 和 pi 之间的值。这不是模棱两可的，所以我认为问题不在这里。似乎我在某处可能有数学错误，但我看不出我的推理有什么漏洞......

EDIT2：对于任何不知道欧拉旋转如何工作的人来说，它是这样的：

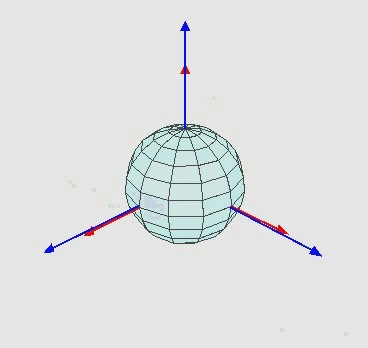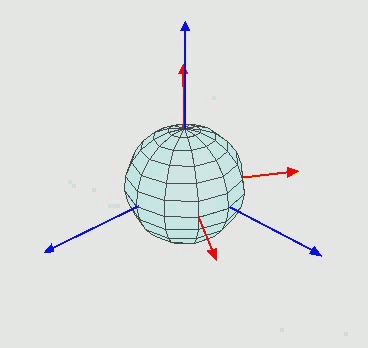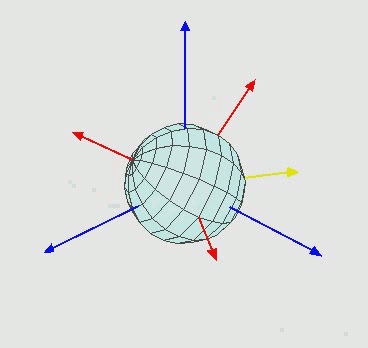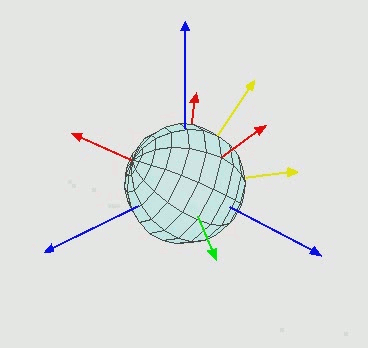
也就是说，绕Z旋转，然后绕新的X轴 ( X' ) 旋转，然后绕新的Z''轴旋转。

因此，我一直在研究SensorEvent文档，试图了解如何确定相对于手机给定轴的北方向。我画了一张小图来说明我对坐标系如何工作的概念：

因此，如果世界坐标是x、y和z，其中磁北沿z并且y指向天空，而手机的坐标是Px、Py和Pz，那么我希望能够计算投影每个向量到另一个向量。

看起来 SENSOR_TYPE_ROTATION_VECTOR 可能是正确的选择，但似乎这并没有给我足够的信息来获得所有这些预测。我是否应该标准化 ROTATION_VECTOR 并将其添加到我关心的轴上，然后拉出组件？

另一个大的单个传感器似乎是 SENSOR_TYPE_ORIENTATION，但我也不清楚如何处理这些值。如果我想知道真实世界坐标系在Py上的三个投影，我是否只需沿给定坐标旋转 [0, 1, 0] ，如下所示：

我刚刚从通用旋转公式中获得了这些公式（因为它正在旋转单位向量，所以您只需选择中心列）。我认为变量 Py 的组成部分将是x，y和z到Py的投影，但我有倒退吗？相反，它是Py在三个现实世界轴上的投影吗？

最后，我注意到有一个 getRotationMatrixFromVector() 选项，它似乎为你计算了这些预测，但我再次不确定我是否有完全倒退的情况。如果我想知道x的三个投影。y和z到Py上，我得到旋转矩阵的第二列还是第二行？

（对于可能是一个非常简单的问题的非常冗长的版本，我认为对于未来困惑的人来说，对坐标系非常明确会更好，这是我的主要困惑点）。

我正在使用 jPCT 库开发 FPS。所有 FPS 都需要的一件事是通过将鼠标向上/向下拉得太远来防止玩家向后看。目前，我正在使用 jPCT 网站上的一些示例代码来跟踪相机中添加了多少角度，但我担心所有角度都以弧度表示的舍入问题。我可以从 jPCT 的相机中得到一个旋转矩阵，我知道它包含的信息可以计算出玩家看起来有多“高”，但我不知道如何将它从矩阵中取出。

我会在旋转矩阵中寻找什么，它会告诉我玩家是否看起来更“向上”而不是“向上”而不是“向下”而不是向下？

给定一个任意的 4x4 变换矩阵，我如何找出旋转中心？