问题标签 [taylor-series]

我需要找到变量 s 的值，以便涉及 s 的表达式的泰勒展开：

1. 在除 0 阶以外的尽可能多的系数中具有最小值（最好是零，但由于二进制最小值就足够了）（最好多于一个最小系数，但第 2 和第 3 具有优先权）。

2. 报告满足区域内条件的 s 的最佳 n 值（即显示 s 的 3 个最佳值以及每个值的系数）。

我不知道如何在Series[]不收到错误的情况下将命令的输出输入到任何其他mathematica 命令中，更不用说如何实际解决问题了。我正在使用的方程太复杂，无法在此处发布（可以扩展的多区域但连续的多项式表达式）。有谁知道为此使用什么命令？

我目前正在尝试计算函数 x^(1/2) 的泰勒级数之和（这就是它在 Wolfram 中的样子：http ://www.wolframalpha.com/input/?i=taylor+series+ x%5E%281%2F2%29）这是所需的公式：http: //i.imgur.com/YvVOQIR.png

我在计算二项式系数时遇到问题。我将其分为两部分（分母中的分子和阶乘）。分子总是计算为 0 值（除了初始化应该为 1 的一次）。

编辑：将 int 更改为双精度（此处也更新了代码），效果很好并编辑了代码：

我正在尝试制作一个程序来评估泰勒级数（如果您不知道，请在下面描述）到第 n 阶。但是，要做到这一点，我需要评估一个函数（我保存在 中Y1）及其第 n 个导数。我尝试使用nDeriv并将其作为字符串保存到Y2、Y3等中，但 TI-84 不允许我一次堆叠超过 2 个。有没有人有办法解决这个问题？

泰勒级数

其中O是序列的给定顺序（较高的值给出更精确的结果），f^(n)(a)表示“函数f在该值处的第 n 个导数a”，并且C是要估计的给定常数

给定变量向量 x[1:3] 及其协方差矩阵 V[1:3,1:3] 的估计值，我寻求一种实用程序，它将线性或非线性函数应用于两个或多个变量，例如

x[4] = x[1] + x[2]

x[5] = x[4] / x[3]。

x[4] 和 x[5] 的估计值需要简单的代数。

包括线性变换 x[4] 的协方差矩阵就是 (H * V * H')，其中

H =

可以使用项 a 和 b 的一阶泰勒级数近似来估计添加 x[5] 的协方差矩阵：

H =

在概念上，我知道算法应该如何工作。但这需要大量的编码，特别是如果我在用户界面中尝试某种通用方程解析器。

是否有任何现有的 R 库可以解决这个问题？

我需要计算 mpmath 的“mpf”浮点 bignums 形式的小值的反正弦函数。

我所说的“小”值是例如 e/4/(10**7) = 0.000000067957045711476130884...

这是在我的机器上使用 mpmath 的内置 asin 函数进行测试的结果：

这是一个特殊情况：我使用的数字有点小，所以我问自己是否有一种方法可以在 python 中计算它，在这种特殊情况下实际上优于 mpmath（= 用于小值）。

泰勒级数在这里实际上是一个不错的选择，因为它们对于小参数收敛得非常快。但我仍然需要以某种方式进一步加速计算。

实际上存在一些问题：
1）二进制拆分在这里无效，因为只有当您可以将参数写成小分数时它才会发光。这里给出了一个全精度浮点数。
2) arcsin 是一个非交替序列，因此 Van Wijngaarden 或 sumalt 变换也无效（除非我不知道有一种方法可以将它们推广到非交替序列）。 https://en.wikipedia.org/wiki/Van_Wijngaarden_transformation

我能想到的唯一加速度是切比雪夫多项式。切比雪夫多项式可以应用于 arcsin 函数吗？如何？

点到点的距离：dist = sqrt(dx * dx + dy * dy); 但是 sqrt 太慢了，我不能接受。我找到了一种叫做 Taylor McLaughlin Series 的方法来估计书上两点的距离。但我无法理解以下代码。感谢任何帮助我的人。

我查阅了有关 McLaughlin Series 的相关数据，但我仍然无法理解返回值是如何使用 McLaughlin Series 来估算值的。谢谢大家~

我正在使用泰勒级数来计算sin(). 罪的泰勒级数是：

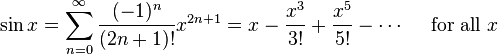
我正在使用的实现如下所示：

据我了解，该代码是j多项式项的近似值（换句话说，近似值是从零到j而不是从零到∞的求和），k在n公式中，当然x是x。

我试图理解那个实现，也就是从上面的公式到代码的转换。我的目标是为该cos()系列编写相同类型的实现。

你能帮我理解吗？

我是编程新手，我无法弄清楚我的代码有什么问题。如果有人可以帮助我了解我的程序出了什么问题，我将不胜感激。我已经在这个问题上工作了两个小时，我知道我正在让它变得比需要的更难。这是我的新代码。我的新输出是 0.000000476837158。

我试图获得任意函数的泰勒级数展开的系数。输入函数必须是变量的形式，输出必须只包含系数。

我尝试了一些 MATLAB 函数，例如“taylor”，但它们以符号形式编写的表达式的形式给出了整个扩展。我知道这样的事情可以在 Mathematica 中完成，但我没有接触过它。因此我不愿意使用 Mathematica 来做这件事。

如果可以建议一个 MATLAB 函数，那将是一个很大的帮助。能够做到这一点的 AC/C++ 库同样会有所帮助。

编辑：我需要泰勒级数展开的系数：我需要找到泰勒级数展开的系数

f(x) = Product_from_{m=1}_to{M}[ {(1-2^{-m})z(1-p)} / {1-z+(1-2^(-m)z( 1-p)}]。

这是我的代码：

但它不起作用并显示此错误：