问题标签 [binary-tree]

我有一个看起来像 (A (B (CD)) (E (F))) 的列表，它代表这棵树：

如何将其打印为 (ABECDF) ？

据我所知，这是：

但它打印：

我对 Common LISP 很陌生，所以可能有一些我应该使用的功能。如果是这样，那么请启发我。

谢谢。

我写了这段代码

我有这些错误

无法在 findmin 上将类型 x.Program.TreeNode' 隐式转换为 'int' //

无法在 findmax 上将类型 x.Program.TreeNode' 隐式转换为 'int'

我的主要内容是正确的还是遗漏的？

以及我如何计算节点、叶子并获得高度（只需要提示）

我对以下代码片段有疑问：

我收到以下错误：

关于如何解决这些错误的任何想法？

嗨，我在 Marc Gravell 的帮助下完成了这段代码

为什么在 BinarySearchTree 中找不到 _left 和 _right？
&
如何更正 BST C# 代码中的隐式转换错误？

，它的二叉搜索树，但现在我遇到了逻辑错误，结果是错误的，我的代码输出如下：

最后两个数字必须给出插入元素的总数 6 但它显示 9

但是我怎么能得到树的高度？！

提前感谢并特别感谢 Marc Gravell。

我有以下来自我不久前参加的关于二叉树（不是 BST）的中序遍历（他们也称之为 pancaking）的学术课程的文本：

中序树遍历

在树的外面画一条线。从根的左侧开始，然后绕过树的外部，最终到达根的右侧。尽可能靠近树，但不要越过树。（把树——它的分支和节点——想象成一个坚固的屏障。）节点的顺序是这条线在它们下面经过的顺序。如果您不确定何时走到节点“下方”，请记住“向左”的节点总是先出现。

这是使用的示例（与下面的树略有不同）

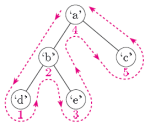
然而，当我在谷歌上搜索时，我得到了一个相互矛盾的定义。例如维基百科示例：

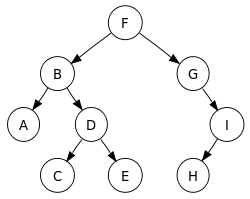
中序遍历序列：A、B、C、D、E、F、G、H、I（leftchild、rootnode、right node）

但根据（我对）定义#1的理解，这应该是

A、B、D、C、E、F、G、I、H

谁能澄清哪个定义是正确的？它们可能都描述了不同的遍历方法，但碰巧使用了相同的名称。我无法相信同行评审的学术文本是错误的，但不能确定。

引用维基百科：

使用传统的二叉树数据结构来实现二叉堆是完全可以接受的。添加可以通过算法解决 的元素时，在二进制堆的最后一级找到相邻元素存在问题......

关于这种算法如何工作的任何想法？

我无法找到有关此问题的任何信息，因为大多数二进制堆都是使用数组实现的。

任何帮助表示赞赏。

最近，我注册了一个 OpenID 帐户，无法编辑我的初始帖子，也无法评论答案。这就是为什么我通过这个答案做出回应。非常遗憾。

引用米奇小麦：

@Yse：您的问题是“如何找到二进制堆的最后一个元素”？

是的。或者更准确地说，我的问题是：“如何找到非基于数组的二进制堆的最后一个元素？”。

引用抑制火：

你在问这个问题时有什么背景吗？（即，您是否正在尝试解决一些具体问题？）

如上所述，我想知道一种“找到基于非数组的二进制堆的最后一个元素”的好方法，这是插入和删除节点所必需的。

引用罗伊的话：

对我来说，使用普通的二叉树结构（使用定义为 [data, pLeftChild, pRightChild] 的 pRoot 和 Node）并添加两个额外的指针（pInsertionNode 和 pLastNode）似乎是最容易理解的。pInsertionNode 和 pLastNode 都将在插入和删除子例程期间更新，以在结构中的数据更改时保持它们的最新状态。这使 O(1) 可以访问结构的插入点和最后一个节点。

是的，这应该有效。如果我没记错的话，当它们的位置由于删除/插入而更改为另一个子树时，找到插入节点和最后一个节点可能会有点棘手。但我会试一试。

引用 Zach Scrivena 的话：

如何执行深度优先搜索...

是的，这将是一个很好的方法。我也会试试看。

我仍然想知道，是否有办法“计算”最后一个节点和插入点的位置。具有 N 个节点的二叉堆的高度可以通过取大于 N 的 2 的最小幂的对数（以 2 为底）来计算。也许也可以计算最深层次的节点数。然后有可能确定必须如何遍历堆才能到达插入点或删除节点。

有谁知道如何计算二叉搜索树的搜索时间（即最坏情况、最佳情况和平均情况）？

我正在寻找在AVL-tree中计算节点余额的最佳方法。我以为我可以正常工作，但是经过一些繁重的插入/更新后，我可以看到它（根本）无法正常工作。

这是一个两部分的问题，第一部分是如何计算子树的高度，我知道定义“节点的高度是从该节点到叶子的最长向下路径的长度。” 我理解它，但我未能实施它。为了让我更加困惑，这句话可以在 wikipedia on tree-heights 上找到“通常，值 -1 对应于没有节点的子树，而 0 对应于具有一个节点的子树。”

第二部分是获取 AVL 树中子树的平衡因子，我对“获取您的树和子树的高度并从中减去”LRRL这个概念没有问题。这被定义为这样的：BALANCE = NODE[L][HEIGHT] - NODE[R][HEIGT]

在维基百科上阅读描述插入 AVL 树的前几行是这样说的：“如果平衡因子变为 -1、0 或 1，那么树仍然是 AVL 形式，不需要旋转。”

然后它继续说“如果平衡因子变为 2 或 -2，则以该节点为根的树是不平衡的，需要进行树旋转。最多需要单轮或双轮旋转来平衡树。” - 我很容易掌握。

但是（是的，总是有一个但是）。

这是令人困惑的地方，文本指出“如果 R 的平衡因子为 1，则意味着插入发生在该节点的（外部）右侧并且需要左旋转”。但是根据我的理解，文本说（正如我所引用的）如果平衡因素在范围内，[-1, 1]那么就不需要平衡了吗？

我觉得我已经非常接近掌握这个概念了，我已经降低了树的旋转，实现了一个正常的二叉搜索树，并且在掌握 AVL 树的边缘，但似乎只是缺少了那个重要的顿悟。

编辑：代码示例优于学术公式，因为我总是更容易掌握代码中的某些内容，但非常感谢任何帮助。

编辑：我希望我可以将所有答案都标记为“已接受”，但对我来说，尼克的答案是第一个让我“啊哈”的答案。

我正在寻找一些用于商业/自由软件项目的树结构示例，无论是现代的还是旧的。我可以在 wikipedia 上看到示例，但我正在寻找更具体的示例以及它们的使用方式。例如，数据库中的主键（根据我的阅读）存储在 BST 结构或 BST 的变体中（请随时纠正我）

我的问题不限于二叉搜索树 (BST)，它可以包括任何变体，例如红黑、AVL 等。

我正在尝试按顺序将节点插入树中。我的功能工作正常......当只有三个节点时。

我有这个代码：

除此之外：

}

我知道这里出了什么问题，我只是不知道如何解决它。这只是覆盖连接到根节点的两个节点。IE

我无法添加节点 4。它只是根据输入覆盖节点 2 或 3。经过调试和一些研究，我不太确定从这里去哪里......

如果有人可以提供帮助，我将不胜感激。