我有以下来自我不久前参加的关于二叉树（不是 BST）的中序遍历（他们也称之为 pancaking）的学术课程的文本：
中序树遍历
在树的外面画一条线。从根的左侧开始，然后绕过树的外部，最终到达根的右侧。尽可能靠近树，但不要越过树。（把树——它的分支和节点——想象成一个坚固的屏障。）节点的顺序是这条线在它们下面经过的顺序。如果您不确定何时走到节点“下方”，请记住“向左”的节点总是先出现。
这是使用的示例（与下面的树略有不同）
然而，当我在谷歌上搜索时，我得到了一个相互矛盾的定义。例如维基百科示例：
中序遍历序列：A、B、C、D、E、F、G、H、I（leftchild、rootnode、right node）
但根据（我对）定义#1的理解，这应该是
A、B、D、C、E、F、G、I、H
谁能澄清哪个定义是正确的？它们可能都描述了不同的遍历方法，但碰巧使用了相同的名称。我无法相信同行评审的学术文本是错误的，但不能确定。
在我对绘图的错误尝试中，这里的顺序显示了应该如何选择它们。
几乎选择了正在绘制的线正上方的节点。
忘记定义，应用算法要容易得多：
void inOrderPrint(Node root)
{
if (root.left != null) inOrderPrint(root.left);
print(root.name);
if (root.right != null) inOrderPrint(root.right);
}
只有三行。重新排列前后订单的顺序。
如果您仔细阅读，您会看到第一个“定义”说从根的左侧开始，并且节点的顺序由您在它们下方经过的时间决定。所以B不是第一个节点，因为你在去的路上从左边经过它，A然后先经过下面 A，然后再往上经过。因此，似乎两个定义都给出了相同的结果。 B
我个人觉得这个讲座很有帮助。
两种定义都给出相同的结果。不要被第一个例子中的字母所迷惑——看看路径上的数字。第二个例子确实使用字母来表示路径 - 也许这就是让你失望的原因。
例如，在您的示例顺序中显示您认为第二棵树将如何使用第一棵树的算法进行遍历，您将“D”放在“B”之后，但您不应该这样做，因为仍有一个左侧子节点D 可用（这就是为什么第一项说“这条线在它们 下面经过的顺序”。
我认为第一个以 为根的a二叉树是一个构造不正确的二叉树。
尝试实现树的所有左侧都小于根，树的所有右侧大于或等于根。
这可能会迟到，但它可能对以后的任何人都有用..您只需要忽略虚拟或空节点，例如节点 G 有一个左空节点..考虑到这个空节点将使一切正常..
正确的遍历将是：叶节点（不是根节点）尽可能左
F 是根还是左，我不确定
但根据（我对）定义#1的理解，这应该是
A, B, D, C, E, F, G, I, H
不幸的是，您的理解是错误的。
每当您到达一个节点时，您必须先下降到一个可用的左节点，然后再查看当前节点，然后再查看可用的右节点。当您在 C 之前选择 D 时，您没有先下降到左侧节点。
嘿，根据我在wiki中提到的正确顺序遍历的顺序是left-root-right。
直到 A、B、C、D、E、F 我想你已经明白了。现在在根 F 之后，下一个节点是 G，它没有左节点而是右节点，因此根据规则 (left-root-right)，它的 null-g-right。现在 I 是 G 的右节点，但我有一个左节点，因此遍历将是 GHI。这是对的。
希望这可以帮助。
对于内联树遍历，您必须记住遍历的顺序是左节点右。对于上图，您在读取左侧的任何叶（子）节点之前读取父节点时会发生错误。
正确的遍历将是：叶节点（A）尽可能向左，返回父节点（B），向右移动，但由于 D 在其左侧有一个子节点，因此您再次向下移动（C），向后移动到 C 的父节点（D），到 D 的右子节点（E），反向返回根节点（F），移动到右叶节点（G），移动到 G 的叶节点，但是因为它有一个左叶节点，所以移动到那里（H） ，返回父级（I）。
当我将节点列在括号中时，上面的遍历会读取节点。
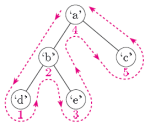
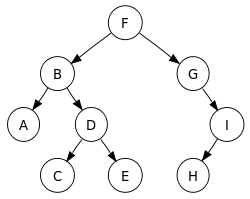
包数据结构；
公共类 BinaryTreeTraversal {
public static Node<Integer> node;
public static Node<Integer> sortedArrayToBST(int arr[], int start, int end) {
if (start > end)
return null;
int mid = start + (end - start) / 2;
Node<Integer> node = new Node<Integer>();
node.setValue(arr[mid]);
node.left = sortedArrayToBST(arr, start, mid - 1);
node.right = sortedArrayToBST(arr, mid + 1, end);
return node;
}
public static void main(String[] args) {
int[] test = new int[] { 1, 2, 3, 4, 5, 6, 7 };
Node<Integer> node = sortedArrayToBST(test, 0, test.length - 1);
System.out.println("preOrderTraversal >> ");
preOrderTraversal(node);
System.out.println("");
System.out.println("inOrderTraversal >> ");
inOrderTraversal(node);
System.out.println("");
System.out.println("postOrderTraversal >> ");
postOrderTraversal(node);
}
public static void preOrderTraversal(Node<Integer> node) {
if (node != null) {
System.out.print(" " + node.toString());
preOrderTraversal(node.left);
preOrderTraversal(node.right);
}
}
public static void inOrderTraversal(Node<Integer> node) {
if (node != null) {
inOrderTraversal(node.left);
System.out.print(" " + node.toString());
inOrderTraversal(node.right);
}
}
public static void postOrderTraversal(Node<Integer> node) {
if (node != null) {
postOrderTraversal(node.left);
postOrderTraversal(node.right);
System.out.print(" " + node.toString());
}
}
}
包数据结构；
公共类节点{
E value = null;
Node<E> left;
Node<E> right;
public E getValue() {
return value;
}
public void setValue(E value) {
this.value = value;
}
public Node<E> getLeft() {
return left;
}
public void setLeft(Node<E> left) {
this.left = left;
}
public Node<E> getRight() {
return right;
}
public void setRight(Node<E> right) {
this.right = right;
}
@Override
public String toString() {
return " " +value;
}
}
preOrderTraversal >> 4 2 1 3 6 5 7 inOrderTraversal >> 1 2 3 4 5 6 7 postOrderTraversal >> 1 3 2 5 7 6 4
void
inorder (NODE root)
{
if (root != NULL)
{
inorder (root->llink);
printf ("%d\t", root->info);
inorder (root->rlink);
}
}
这是递归定义中序遍历最简单的方法，只需在主函数中调用该函数即可得到给定二叉树的中序遍历。
预购是正确的，订单是nt