问题标签 [square-root]
For questions regarding programming in ECMAScript (JavaScript/JS) and its various dialects/implementations (excluding ActionScript). Note JavaScript is NOT the same as Java! Please include all relevant tags on your question; e.g., [node.js], [jquery], [json], [reactjs], [angular], [ember.js], [vue.js], [typescript], [svelte], etc.
java - 平方根字符/符号
我想知道平方根符号的字符代码在java中是什么?也就是说,我希望能够在一串其他字符内的屏幕上打印一个平方根符号,或者作为按钮上的标签。
android - 如何在android中包含下图所示的平方根符号?
我需要在我的 android 中包含以下平方根符号作为 Button 控件中的文本资源。有什么猜测吗?
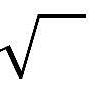
math - 由于浮点舍入误差,非整数的平方根会变成整数吗?
在另一个不相关的 Internet 论坛上,有人询问如何检查给定数字的平方根是否为整数。现在,这本身就是一个微不足道的家庭作业问题,但我开始怀疑这种幼稚的方法是否在所有情况下都是正确的。也就是说,在伪代码中:
是否可以输入这样的x,它x本身不是整数(或不是另一个整数的平方的整数),而是由于浮点错误而sqrt(x) 成为整数?
c++ - 元整数平方根中的无限递归
再会,
我的一个朋友正在询问将整数平方根函数转换为元函数。这是原始功能:
我使用 编写了一个元版本constexpr,但他说由于某种原因他不能使用新功能:
所以我认为将其转换为以递归方式调用它的模板结构应该不难:
不幸的是,这导致了无限递归(在 GCC 4.6.1 上),我无法弄清楚代码有什么问题。这是错误:
谢谢大家,
python - 打印任意数量的浮点数
如何float在 python 中打印超过 10 个数字的 a?现在,什么时候做
print sqr_newton(10, 3, 0.001)(其中 sqr_newton 是牛顿的平方根算法;返回一个浮点数)
它只在小数点后给出这么多位数......我怎样才能得到更多?
c++ - 给定 r^2,有没有一种有效的方法来计算 r^3?
第二行可以用更快的东西代替吗?不涉及的东西sqrt?
math - 求 2 的平方根到小数点后 100 位以上
我试图通过使用此处描述的牛顿方法来完成这项工作:wiki使用以下代码,但问题是它只能给出精确的结果,最多小数点后 16 位。我试图增加迭代次数,结果还是一样。我从 1 的初始猜测开始。那么我怎样才能提高答案的准确性(最多 100 位或更多小数位)?谢谢。代码:
c++ - 在整数数组中查找顶部 log(n) 或顶部 sqt(n) 值
你明白这个问题的意思吗
在小于线性时间的整数数组中查找顶部 log(n) 或顶部 sqt(n) 值。
如果你不这样做,这里是http://www.careercup.com/question?id=9337669的问题。
您能否帮助我理解这个问题,然后可能会得到解决。(虽然一旦我明白我也可能会解决它)
谢谢你的时间。
java - Java中的精确平方根
在Java中存储无理数(如平方根)的最佳方法是什么?我需要很高的精度(超过 100 位),所以 float 和 double 不会很好。是大十进制吗?我以前使用过它,但遇到了奇怪的问题,不过它可能只是我的代码。我的代码非常复杂,所以我想确保 BigDecimal 是正确的方法,然后再重新处理其他内容。
c++ - 如何改进小值的定点平方根
我正在使用 Dobb 博士的文章“ Optimizing Math-Intensive Applications with Fixed-Point Arithmetic ”中描述的 Anthony Williams 的定点库,使用Rhumb Line 方法计算两个地理点之间的距离。
当点之间的距离很长(大于几公里)时,这很有效,但在较小的距离时效果很差。最坏的情况是当两个点相等或接近相等时,结果是 194 米的距离,而我需要在 >= 1 米的距离处至少 1 米的精度。
通过与双精度浮点实现进行比较,我发现了函数的问题,该fixed::sqrt()函数在较小的值下表现不佳:
通过将其视为特殊情况来纠正结果fixed::sqrt(0)是微不足道的,但这并不能解决小的非零距离的问题,其中误差从 194 米开始并随着距离的增加收敛到零。我可能需要至少一个数量级的精度提高到零。
该fixed::sqrt()算法在上面链接的文章的第 4 页上进行了简要说明,但我很难遵循它,更不用说确定是否可以改进它。该函数的代码复制如下:
注意m_nVal是内部定点表示值,它是一个int64_t并且表示使用Q36.28格式(fixed_resolution_shift= 28)。该表示本身具有至少 8 位小数的足够精度,并且作为赤道弧的一小部分适用于大约 0.14 米的距离,因此限制不是定点表示。
使用恒向线法是该应用程序的标准机构建议,因此无法更改,并且在任何情况下,在应用程序的其他地方或将来的应用程序中都可能需要更准确的平方根函数。
问题:是否有可能提高fixed::sqrt()算法对小的非零值的准确性,同时仍保持其有界和确定性收敛?
附加信息 用于生成上表的测试代码:
结论 根据 Justin Peel 的解法和分析,并与《被忽视的定点算术艺术》中的算法进行比较,我将后者改编如下:
虽然这提供了更高的精度,但我需要的改进并没有实现。仅 Q36.28 格式就提供了我需要的精度,但不可能在不损失几位精度的情况下执行 sqrt()。然而,一些横向思维提供了更好的解决方案。我的应用程序根据某个距离限制测试计算出的距离。事后看来,相当明显的解决方案是测试距离的平方与极限的平方!