10

我正在实现触摸屏 UI 的滚动行为，但此刻我太累了，无法将注意力集中在一些所谓的微不足道的数学上：

y (distance/velocity)
|********
|        ******
|              ****
|                  ***
|                     ***
|                        **
|                          **
|                            *
|                             *
-------------------------------- x (time)

f(x)->?

UI 应该允许用户在任何方向上拖动和“扔”视图，并且即使在他从屏幕上松开手指后也可以让它滚动一段时间。它有点动量，取决于用户在松开手指之前拖动的速度。

所以我有一个起始速度（v0），每 20 毫秒我滚动一个相对于当前速度的量。每次滚动迭代时，我都会稍微降低速度，直到我停止它时它低于阈值。当我将其减少一个固定量（线性）时，它看起来不正确，所以我需要对负加速度进行建模，但未能提出一个体面的简单公式来计算我必须降低速度的量在每次迭代中。

更新：

感谢您到目前为止的回复，但我仍然没有设法从反馈中获得令人满意的功能。我可能没有很好地描述所需的解决方案，所以我将尝试给出一个真实世界的例子来说明我想做什么样的计算：

假设某辆汽车在某条街道上行驶，驾驶员将刹车踩到最大，直到汽车停下来。驾驶员在同一条街道上多次使用同一辆车执行此操作，但开始以不同的速度制动。当汽车减速时，我希望能够仅根据当前速度计算出它在一秒钟后的速度。对于这个计算，当驾驶员开始休息时汽车以何种速度行驶并不重要，因为所有环境因素都保持不变。当然，公式中会有一些常数，但是当汽车减速到 30 m/s 时，它会在下一秒走相同的距离，无论驾驶员开始刹车时是在 100 还是 50 m/s 行驶. 因此，从击中休息开始的时间也不会是函数的参数。在一定速度下的减速度总是相同的。

在这种情况下，假设减速度、质量、摩擦等一些任意常数并忽略空气阻力等复杂影响，你如何计算一秒钟后的速度？我只追求动能和它由于打破汽车的摩擦而消散。

更新 2 我现在看到汽车的加速度是线性的，这实际上不是我想要的。明天我会清理它并尝试新的建议。感谢您迄今为止的意见。

4

15 回答 15

8

[简短答案（假设C语法）]

double v(double old_v, double dt) {
    t = t_for(old_v); 
    new_t = t - dt; 
    return (new_t <= 0)?0:v_for(t);
}

double t_for(double v)并且double v_for(double t)是来自 v-to-t 双向映射（数学意义上的函数）的返回值，它是任意的，但它是单调的并且定义为v >=0（因此有一个点 where v=0）。一个例子是：

double v_for(double t) { return pow(t, k); }
double t_for(double v) { return pow(v, 1.0/k); }

哪里有：

  1. k>1随着时间的推移，减速度以模数递减.
  2. k<1随着时间的推移，减速度以模数增加。
  3. k=1给出恒定的减速。

[更长的一个（有基本原理和情节）]

所以目标本质上是：

  1. 找到一个函数v(t+dt)=f(v(t),dt)，它采用当前速度值v和时间增量dt并返回当前速度t+dt（它不需要实际指定t，因为v(t)已知并作为参数提供，并且dt只是时间增量）。换句话说，任务是实现double next_v(curr_v, dt);具有特定属性的例程（见下文）。

  2. [请注意]有问题的函数具有返回相同结果的有用（和期望）属性，而不管先前速度变化的“历史”如何。这意味着，例如，如果一系列连续速度是 [100, 50, 10, 0]（对于起始速度v0=100），则任何其他大于此的序列都将具有相同的“尾巴”： [150, 100, 50, 10, 0]（对于起始速度v0=150）等。换句话说，无论起始速度如何，所有速度-时间图都将有效地相互复制，只是沿时间轴偏移各自的值（见下图，注意线之间的图部分t=0.0是t=2.0相同的）。

  3. 此外，加速度w(t)=dv(t)/dt必须是时间的递减函数t（为了我们在这里建模的移动 GUI 对象的视觉上令人愉悦和“直观”的行为）。

提议的想法是：

  1. 首先，您选择具有所需属性的单调速度函数（在您的情况下，它逐渐减小加速度，但如下例所示，使用“加速”函数更容易）。这个函数也不能有一个上限，这样你就可以将它用于任何大的速度值。此外，它必须有一个速度为零的点。一些例子是：（v(t) = k*t不完全是你的情况，因为减速k在这里是恒定的），v=sqrt(-t)（这个没问题，在区间上定义t <= 0）。

  2. 然后，对于任何给定的速度，您在上述函数的图上找到具有该速度值的点（将有一个点，因为该函数没有绑定，并且只有一个，因为它是单调的），按时间增量向更小的速度前进值，从而获得下一个。迭代将逐渐（并且不可避免地）将您带到速度为零的地步。

  3. 基本上就是这样，甚至不需要生成一些“最终”公式，对时间值或初始（非当前）速度的依赖消失了，编程变得非常简单。

对于两个简单的情况，这个小 Python 脚本会生成下面的图（给定1.0的初始速度10.0为无论您以何种速度开始减速（减速），您都在沿着相同的曲线相对“移动”到速度为（变为）零的点：

import numpy
import pylab

import math


class VelocityCurve(object):
    """
    An interface for the velocity 'curve'.
    Must represent a _monotonically_ _growing_
        (i.e. with one-to-one correspondence
        between argument and value) function
        (think of a deceleration reverse-played)
    Must be defined for all larger-than-zero 'v' and 't'
    """
    def v(self, t):
        raise NotImplementedError

    def t(self, v):
        raise NotImplementedError



class VelocityValues(object):

    def __init__(self, v0, velocity_curve):
        assert v0 >= 0
        assert velocity_curve

        self._v = v0
        self._vc = velocity_curve

    def next_v(self, dt):
        t = self._vc.t(self._v)
        new_t = t - dt

        if new_t <= 0:
            self._v = 0
        else:
            self._v = self._vc.v(new_t)

        return self._v


class LinearVelocityCurve(VelocityCurve):

    def __init__(self, k):
        """k is for 'v(t)=k*t'"""
        super(LinearVelocityCurve, self).__init__()

        self._k = k

    def v(self, t):
        assert t >= 0
        return self._k*t

    def t(self, v):
        assert v >= 0
        return v/self._k


class RootVelocityCurve(VelocityCurve):

    def __init__(self, k):
        """k is for 'v(t)=t^(1/k)'"""
        super(RootVelocityCurve, self).__init__()

        self._k = k

    def v(self, t):
        assert t >= 0
        return math.pow(t, 1.0/self._k)

    def t(self, v):
        assert v >= 0
        return math.pow(v, self._k)


def plot_v_arr(v0, velocity_curve, dt):
    vel = VelocityValues(v0, velocity_curve)
    v_list = [v0]

    while True:
        v = vel.next_v(dt)
        v_list.append(v)

        if v <= 0:
            break

    v_arr = numpy.array(list(v_list))
    t_arr = numpy.array(xrange(len(v_list)))*dt

    pylab.plot(t_arr, v_arr)


dt = 0.1

for v0 in range(1, 11):
    plot_v_arr(v0, LinearVelocityCurve(1), dt)

for v0 in range(1, 11):
    plot_v_arr(v0, RootVelocityCurve(2), dt)


pylab.xlabel('Time ')
pylab.ylabel('Velocity')

pylab.grid(True)

pylab.show()

这给出了以下图（线性减速度（即恒定减速度）的线性图，“曲线” - 对于“平方根”的情况（参见上面的代码））：

另外请注意，要运行上述脚本，需要安装pylab、numpy和朋友（但仅对于绘图部分，“核心”类不依赖任何东西，当然可以单独使用）。

PS 通过这种方法，人们可以真正“构建”（例如，为不同的t间隔增加不同的函数，甚至平滑手绘（记录的）“人体工程学”曲线）他喜欢的“拖动”：）

于 2010-02-20T02:47:24.663 回答
5

阅读评论后，我想改变我的答案：将速度乘以 k < 1，如 k = 0.955，使其呈指数衰减。

解释（带有图表和可调方程！）如下......

我将您原始问题中的图表解释为显示速度保持在起始值附近，然后越来越快地下降。但是，如果你想象一本书滑过桌子，它会迅速从你身边移开，然后放慢速度，然后慢慢停下来。我同意@Chris Farmer要使用的正确模型是与速度成正比的阻力。我将采用这个模型并得出我上面建议的答案。我提前为这篇文章的长度道歉。我相信数学更好的人可以大大简化这一点。 另外，我直接将图表的链接放入其中，链接中有一些 SO 解析器不喜欢的字符。 网址现已修复。

我将使用以下定义：

x -> time
a(x) -> acceleration as a function of time
v(x) -> velocity as a function of time
y(x) -> position as a function of time
u -> constant coefficient of drag
colon : denotes proportionality

我们知道，由于阻力而产生的力与速度成正比。我们也知道力与加速度成正比。

a(x) : -u v(x)        (Eqn. 1)

减号确保加速度与当前行进方向相反。

我们知道速度是综合加速度。

v(x) : integral( -u v(x) dx )        (Eqn. 2)

这意味着速度与其自身的积分成正比。我们知道e^x满足这个条件。所以我们假设

v(x) : e^(-u x)        (Eqn. 3)

当我们求解方程中的积分时，指数中的阻力系数是这样的。2取消u返回方程。3.

现在我们需要弄清楚 的值u。正如所@BlueRaja指出的，e^x永远不会等于零，无论 x 是多少。但是对于足够负的 x，它接近于零。让我们考虑 1% 的原始速度被“停止” （您对阈值的想法），假设我们想在 x = 2 秒内停止（您可以稍后调整）。那么我们需要解决

e^(-2u) = 0.01        (Eqn. 4)

这导致我们计算

u = -ln(0.01)/2 ~= 2.3        (Eqn. 5)

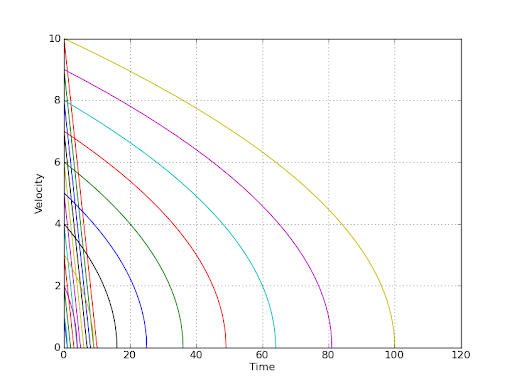
让我们绘制图表v(x)。

看起来它在 2 秒内呈指数衰减到一个小值。到目前为止，一切都很好。

我们不一定要在 GUI 中计算指数。我们知道我们可以很容易地转换指数基，

e^(-u x) = (e^-u)^x        (Eqn. 6)

我们也不想以秒为单位跟踪时间。我们知道我们有 20 毫秒的更新速率，所以让我们定义n一个滴答率为 50 滴答/秒的时间滴答。

n = 50 x        (Eqn. 7)

用 Eqn 代入 u 的值。5 进入方程式。6，结合方程式。7，并代入Eqn。3，我们得到

v(n) : k^n, k = e^(ln(0.01)/2/50) ~= 0.955        (Eqn. 8)

让我们用我们新的 x 轴在 timeticks 中绘制它。

同样，我们的速度函数与在所需迭代次数中衰减到 1% 的东西成正比，并遵循“在摩擦影响下滑行”模型。我们现在可以将我们的初始速度乘以v0Eqn。8 得到任何时间步长 n 的实际速度：

v(n) = v0 k^n        (Eqn. 9)

请注意，在实现中，没有必要跟踪 v0！我们可以将封闭形式转换v0 * k^n为递归得到最终答案

v(n+1) = v(n)*k        (Eqn. 10)

这个答案满足了你不关心初始速度的约束——下一个速度总是可以只使用当前速度来计算。

值得检查以确保位置行为有意义。遵循这种速度模型的位置是

y(n) = y0 + sum(0..n)(v(n))        (Eqn. 11)

方程式中的总和。使用方程 9 的形式很容易求解11 。使用索引变量 p：

sum(p = 0..n-1)(v0 k^p) = v0 (1-k^n)/(1-k)        (Eqn. 12)

所以我们有

y(n) = y0 + v0 (1-k^n)/(1-k)        (Eqn. 13)

y0 = 0让我们用和绘制它v0 = 1。

于是我们看到一个急速的远离原点，顺着优美的海岸停了下来。我相信这个图表比你的原始图表更忠实地描述了滑动。

通常，您可以k使用等式进行调整

k = e^(ln(Threshold)/Time/Tickrate)        (Eqn. 14)
where:
Threshold is the fraction of starting velocity at which static friction kicks in
Time is the time in seconds at which the speed should drop to Threshold
Tickrate is your discrete sampling interval

（感谢@poke您展示了 Wolfram Alpha 用于绘图 - 这非常甜蜜。）

旧答案

将速度乘以 k < 1，如 k = 0.98，使其呈指数衰减。

于 2010-02-19T18:56:16.480 回答
4

当汽车减速时，我希望能够仅根据当前速度计算出它在一秒钟后的速度。

这就是加速度的定义。例如，如果加速度是a = -9 meters/sec/sec，而现在的速度是20 meters/sec，那么从现在开始 1 秒后速度将是11 meters/sec。

换句话说，从Δv现在到t几秒后的速度变化（假设加速度不变）将是

Δv = a*t

意味着在任何时候的速度（经典物理）方程t，给定初始速度t=0（这个速度被称为 v 0）是

v(t) = v0+ a*t

使用你在微积分课的前两周学到的知识，你还可以从上面的等式中得到x(t)（汽车在时间的距离t）的等式；这会给你

x(t) = x0 + v0 *t + 0.5*a*t2

（也可以在没有微积分的情况下得出这个，见这里）

最后，如果您是为游戏而不是物理模拟执行此操作（这意味着您不需要精确的结果），您将只想更改每帧的位置和速度，而不是每帧重新计算位置。为此，您需要在每一帧执行以下操作，假设速度（和加速度）以像素每秒（-每秒）为单位测量：

velocity_new = velocity_old + acceleration/frames_per_second
position_new = position_old + velocity_old/frames_per_second
于 2010-02-20T01:54:17.517 回答
2

如果您想像您在 mtrw 的回答中所说的那样增加减速，并且您对物理现实主义不是很挑剔，那么下面的等式可能就是您要寻找的：

V(t+dt) = V(t) - K1 + K2 x V(t)

V(t)= 当前速度 V(t+dt)= 下一次增量的速度 K1 和 K2 是您校准的常数。只需确保 (K2 x Vmax) < K1，否则您将高速加速。

如果仍然感觉不对，请尝试 V(t+dt) = V(t) - K1 + K2 xf(V(t))

其中 f(x) 是您选择的单调递增函数，可能是平方或平方根，具体取决于您想要感受的地方。只需确保 (K2 xf(V(t))) < K1 对于每个可能的 V(t)。

（单调递增函数意味着当 x 增加时 f(x) 总是增加）

于 2010-02-20T02:47:47.813 回答
2

似乎您正在寻找随着时间的推移而增加的减速。

尝试计算

Delta_v = -(A*t + B), 选择适合您的合理常数 A 和 B。

t 是到该点的总时间。

通过添加来改变你的速度Delta_v。

这基本上对应于线性负加速度。

您基本上可以选择任何随时间增加的函数（例如 f(t)）

并计算

Delta_v = -f(t)

An appropriate choice for f(t) would give you the effect you desire.

您可以使用的一些示例：

f(t) = At + B.
f(t) = A*exp(Bt)

当然，您将不得不尝试一下并尝试找出正确的常数。

于 2010-02-19T19:29:58.890 回答
2

我也会添加一个想法。看起来您不想要恒定（负）加速度。这将导致如下等式：

v(t) = v(0) + a*t,

其中a是负加速度，t是时间，v(t)是 时间 处的速度t。这给了你：

v(t2) - v(t1) = a(t2-t1),

这意味着对于给定的Δt，速度差等于aΔt，一个常数。

您可能正在寻找的是一个“摩擦”术语，它取决于当前的速度。在该假设下，速度变化率与当前速度成正比：

d v(t) / d t = -b*v(t).

解决上述问题很容易，你得到： v(t) = v(0) e −bt。

积分这个方程，我们得到 x(t) = v(0)(1−e −bt ) / b，其中 x 是位置。v(0) = 1, b = 0.1的位置图1看起来像你可以使用的东西。使用 b 的值，并在等式中添加比例因子可能是您想要做的。

1 http://www.wolframalpha.com/input/?i=plot+%281+-+1+e^%28-0.1+x%29+%29+%2F+0.1+for+x+%3D+0+to+100

于 2010-02-20T03:36:25.780 回答
2

您可以每次迭代将速度降低一个常数。示例：您以 50 的速度开始，下一次迭代是 40，然后是 30、20、10，停止。这将代表一个恒定的“摩擦”，与速度无关，这实际上非常接近现实（参见Wikipedia 上的摩擦）。

如果您不喜欢这种外观，则需要使摩擦力取决于速度。我会假设一个friction = base-friction + (coefficient * velocity)系数相当小的线性关系就足够了。

于 2010-02-19T21:16:54.857 回答
1

速度的非线性变化意味着加速度不是恒定的。非恒定加速度意味着系统受到jerk的影响。取所有加速度方程并添加“(1/6)jt 3 ”。修复 a，并给 ja 一个小的负值，直到 v 达到 0。

于 2010-02-20T02:57:36.720 回答
0 
y(x) = y0 - a * e ^ ( k * x )

其中y0是起始常数，a和k是因子。

示例图。

于 2010-02-20T17:56:25.717 回答
0

I would cut down velocity as something like v=v*0.9 Then i would have a velocity which is considered the stopped velocity. This way the object would come to rest eventually and not continue consuming resources as moving. so something like for(v=startingVelocity;v<1.0;v*=0.9) { x+=v; }

于 2010-02-19T19:38:29.087 回答
0

我试过这个，它有效（在 Ruby 中）。不确定数学是否合理，但输出看起来正确，这意味着您越靠近中心越快：

velocity=100;
(100.downto(0)).each { |distance_from_black_hole |  velocity=velocity+9.8/distance_from_black_hole; puts velocity; }
于 2010-02-20T03:11:38.293 回答
0

关于汽车示例的一些非编程讨论。

首先，我假设驾驶员不能使制动器在速度上锁定。

大多数新驾驶员学习的第一件事（或者可能是第二或第三件事）是制动时的自然趋势是将制动踏板保持在固定位置。结果是当汽车从缓慢移动到停止时突然向前倾斜。发生这种情况是因为制动器正在从动态摩擦（制动力与制动压力成正比）转变为静态摩擦（制动力正在恢复汽车的前进动量）。这种突然的加速跳跃是令人不快的，新司机学会了在减速结束时踩踏板停止。

这种行为掩盖了另一个特殊性，但在手动变速箱汽车的正常加速过程中可以注意到这一点。在加速（或减速）时，如果驾驶员突然将变速箱从档位弹出，所有乘客都会突然向前倾斜。实际发生的情况是，将他们压在座椅靠背上的加速力突然消失了，他们弹回了中立的坐姿。一种更舒适的驾驶方式是逐渐踩下离合器，从而逐渐消除发动机的动力。

在这两种情况下，更美观的驾驶风格包括平滑加速，消除突然跳跃。这基本上是谈论连续二阶导数的另一种方式。几乎任何具有此属性的运动都会显得很自然。

于 2010-02-20T04:40:30.987 回答
0

加速度是速度的一阶导数和距离的二阶导数。对于某些常数 C 和 k，您的图看起来像二阶抛物线，例如 Ck*x^2。如果 y 真的是距离，则需要 a=-2k，如果 y 是速度，则需要 a=-2kx。在任何一种情况下，速度 v(x) = V0 + a(x)*x。（其中 x 实际上是时间。我遵循您的约定而不使用 t。）

于 2010-02-19T19:55:19.723 回答
0

您可以跟踪速度并每次将其降低速度的一小部分。我相信这会很好地模拟摩擦。

于 2010-02-19T18:56:44.483 回答
0 
加速度=（力/质量）
速度=（加速度*时间）
（来自用户手指的力）= 加速度 / 质量 = 速度 / 时间
  1. 给视图一个质量（调整它直到事情看起来合理，然后让用户调整它）
  2. 确定一些新的力量（拖动）
  3. 给新的力量（拖动）一个幅度（调整到合理，让用户调整它）
  4. 将新的力施加到物体上并观察它减速
于 2010-02-19T18:59:30.630 回答