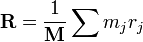3

我正在研究 C# 2d 软体物理引擎，我需要将质量分配给给定的对象顶点：顶点列表（x，y 位置）、对象的总质量和质心。

质心如下：

替代文字

在哪里，

R = center of mass
M = total mass
mj = mass of vertex j
rj = position of vertex j

我需要一种算法，可以在给定 R、M 和 rj 的情况下近似每个 mj。

编辑：我只是想澄清一下，我知道有无限的解决方案。我正在寻找一种快速算法，可以找到一组 mj（这样它们每个都足够接近 mj = M/[顶点数]，并且“足够”被定义为一些小的浮点阈值）。

此外，每个对象将包含大约 5 到 35 个点。

4

4 回答 4

2

您可以按如下方式计算均匀密集多边形的 CM：将 N 个顶点从 0..N-1 编号，并循环处理它们，以便顶点 N 环绕到顶点 0：

total_area = sum[i=0..N-1]( X(p[i],p[i+1])/2 )
CM = sum[i=0..N-1]( (p[i]+p[i+1])*X(p[i],p[i+1])/6 ) / total_area

   where X(p,q)= p.x*q.y - q.x*p.y  [basically, a 2D cross product]

如果多边形是凸的，则 CM 将在多边形内部，因此您可以合理地开始将区域切成三角形，如馅饼，CM 位于中心。您应该能够在不更改 CM 的情况下用其质量的三分之一来加权三角形的每个顶点——但是，这仍然会在整个多边形的 CM 处留下三分之一的总质量。尽管如此，将质量传递缩放 3/2 应该可以让您在两个“外部”顶点之间分割每个三角形的质量。因此，

area[i] = X( (p[i]-CM), (p[i+1]-CM) ) / 2
   (this is the area of the triangle between the CM and vertices i and i+1)

mass[i] = (total_mass/total_area) * (area[i-1] + area[i])/2

请注意，这种质量传递是非常“非物理的”——如果没有别的，如果从字面上看，它会严重破坏惯性矩。但是，如果您需要在顶点之间分配质量（例如某种俗气的爆炸），并且您不想在这样做时破坏 CM，那么这应该可以解决问题。

最后，有几个警告：

  • 如果您不为此使用实际的 CM，它将无法正常工作
  • 在凹面物体上使用它是危险的；你有可能以负质量结束
于 2010-01-25T10:08:49.857 回答
1

计算自由度：对于D维度空间中的点，您有D+1方程[+] 和单独粒子n的未知数。n如果n>D+1你沉没了（除非你有比你告诉我们更多的信息：对称约束、高阶矩等......）。

编辑：我的早期版本假设你有m_is 并且正在寻找r_is。当您拥有r_is 并想要m_is 时，情况会稍微好一些。

[+]您在上面列出的那个（实际是D单独的等式）和M = \sum m_j

阿里乌 说：

哦，对不起，我误解了你的问题。我以为你在问我是否在为诸如圆环、甜甜圈或环（带有切口的对象......）之类的对象建模。我正在用外壳（如气球或气泡）对身体进行建模。我不需要比这更复杂的东西。

现在我们正在取得进展。你确实知道更多。

您可以通过将对象分成相邻点之间的三角形来近似对象的表面积。这个总面积给你平均质量密度。r_i现在找到自由度不足，并根据平均密度和它所属的每个三角形面积的 1/3 为许多 s（我猜是随机绘制的）分配初始质量。然后解析求解剩余系统。如果问题是病态的，您可以绘制一组新的指定点，或者尝试对您已经猜到的群众进行随机游走。

于 2010-01-24T20:31:58.737 回答
1

质心 R 将随着顶点的移动而不断变化。因此，如果您有 10 个顶点，请存储来自 10 个连续“帧”的值 - 这将为您的 10 个未知数提供 10 个方程（假设质量不随时间变化）。

于 2010-01-25T01:47:26.110 回答
0

我会翻转这个问题。也就是说，给定一个密度和物体的位置（当然自然仍然是物体的质心和对应于物体方向的三个矢量，参见欧拉角），在每个顶点处将一个体积与元素（它会随着分辨率而变化，并且对于对象边缘的位置可能是分数）并将密度（d_j）乘以相关的体积（v_j），m_j=v_j * d_j。这种方法应该自然地再次再现物体的质心。

也许我不明白你的问题，但考虑到这最终会产生正确的质量（ Mass = sum(m_j) = sum(v_j * d_j) ），最坏的情况是这种方法应该对你的结果产生验证。

于 2010-01-25T01:26:47.493 回答