如何Ax+Bsin(x)=C根据 A,B 和 C 确定方程的初始猜测？我正在尝试使用 Newton Raphson 解决它。A、B 和 C 将在运行时给出。
为此目的，还有其他方法比牛顿拉夫森更有效吗？
问问题
9967 次
4 回答
4
最佳初始猜测是根本身，因此找到“最佳”猜测并不是真正有效的。
任何猜测最终都会给你一个有效的解决方案，只要f'(x0) != 0对于任何步骤，它只出现在 的零点cos(x)，k*pi + pi/2对于任何整数k。
我会尝试x0 = C * pi，只是看看它是否有效。
但是，您最大的问题是函数的周期性。牛顿的方法对于您的功能来说会很慢（如果它甚至有效），因为sin(x)会x0一遍又一遍地来回移动。
预防：
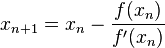
在牛顿的方法中，你注意到f'(xn)分母是多少吗？无限次f'(x)接近。0如果你的f'(x) = 0.0001（或任何接近零的地方，有可能发生），你xn+1会被扔得离xn.
更糟糕的是，由于f'(x)是周期性函数，这可能会一遍又一遍地发生，这意味着牛顿方法甚至可能永远不会收敛于任意x0.
于 2012-04-05T04:08:41.967 回答
1
最简单的“好”近似是假设 sin(x) 近似为零，因此设置：
x0 = C/A
于 2012-04-05T04:14:54.147 回答
0
好吧，如果 A、B 和 C 是实数且不为 0，则(B+C)/A是最高根的上引号和(C-B)/A最低根的下引号，如-1 <= sin(x) <= 1。你可以从这些开始。
于 2015-06-03T15:36:07.873 回答
0
牛顿法适用于任何猜测。问题很简单，如果有一个方程，我猜 x0=100，它的最佳接近解是 x0=2，我知道答案是 2.34*，通过使用世界上的任何猜测，你最终会得到 2.34*方法说选择一个猜测，因为如果没有一个有效的猜测，它将需要许多令人不舒服的解决方案，没有人愿意重复该方法 20 次，猜测解决方案并不难，你只需找到一个临界点 - 例如，3 也是big and 2 太小了，所以答案在 2 和 3 之间，但是如果你猜 2 你猜 50 你仍然会得到正确的解决方案。
于 2017-05-21T19:16:25.527 回答