8

我有一大组 3D 数据点，我想将其拟合到椭圆体中。

我的数学很差，所以我无法在没有任何数学库的情况下实现最小二乘法。

有谁知道或有一段代码可以将椭球拟合到我可以直接插入我的项目的数据中？最好用 C 语言，但从 C++、Java、C#、python 等转换对我来说应该没问题。

编辑：只要能够找到中心也将是一个巨大的帮助。请注意，这些点的间距不均匀，因此取平均值不会导致中心。

4

9 回答 9

8

干得好：

本文描述了将椭圆体拟合到多个维度以及找到椭圆体的中心。希望这可以帮助，

http://www.physics.smu.edu/~scalise/SMUpreprints/SMU-HEP-10-14.pdf

（顺便说一句，我假设这个答案有点晚了，但我想我会为任何偶然发现你的问题以寻找相同内容的人添加这个解决方案:)

于 2011-11-21T17:56:56.010 回答
2

如果您想要最小体积的封闭椭球，请查看这个 SO answer for a bounding ellipsoid。

如果您想要最小二乘意义上的最佳拟合椭圆，请查看此 MATLAB 代码以获取错误椭圆，您可以在其中找到均值偏移 3D 点的协方差矩阵并使用它来构造椭圆。

于 2011-09-01T16:40:24.437 回答
1

考虑到您描述的数据的性质，最小二乘数据拟合可能是一种很好的方法。GNU 科学库包含线性和非线性最小二乘数据拟合例程。在您的情况下，您可以将数据转换为线性空间并使用线性最小二乘法，但这取决于您的实际用例。否则，您将需要使用非线性方法。

于 2011-09-01T16:21:38.427 回答
1

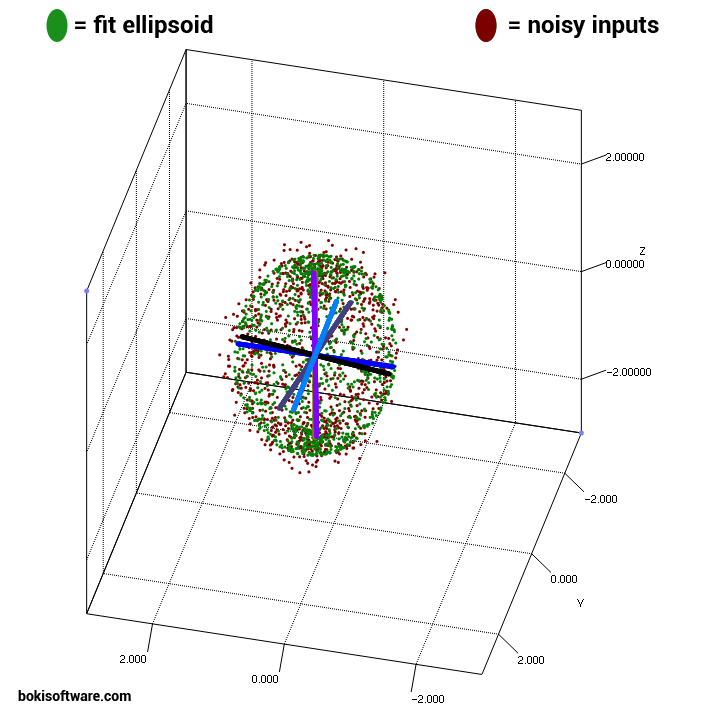
我找不到一个好的基于 Java 的算法来拟合椭圆体，所以我最终自己编写了它。对于具有 2D 点的椭圆有一些很好的算法，但对于具有 3D 点的椭圆体则没有。我尝试了几个不同的 MATLAB 脚本，最终选择了 Yury Petrov 的 Ellipsoid Fit。它适合多项式 Ax^2 + By^2 + Cz^2 + 2Dxy + 2Exz + 2Fyz + 2Gx + 2Hy + 2Iz = 1 的椭球。它不使用任何约束来强制椭球，所以你必须有相当多的点来防止随机二次拟合而不是椭球。除此之外，它工作得非常好。我使用 Apache Commons Math 编写了一个小型 Java 库，该库在 Java 中实现了 Yury Petrov 的脚本。GIT 存储库可以在https://github.com/BokiSoft/EllipsoidFit找到。

0

于 2012-12-23T19:00:20.473 回答
1

我们在这里开发了一组 Matlab 和 Java 代码来拟合椭圆体： https ://github.com/pierre-weiss

您还可以查看我们的开源 Icy 插件。以下教程可能会有所帮助： https ://www.youtube.com/endscreen?video_referrer=watch&v=nXnPOG_YCxw

注意：大多数现有代码都适合通用二次曲线并且不强加椭球形状。为了获得更高的鲁棒性，您需要使用凸编程而不仅仅是线性代数。这是在指定来源中所做的。

干杯，皮埃尔

于 2017-02-15T16:30:36.700 回答
0

我有个主意。大约解决方案，不是最好的，但会在里面保留点。在 XY 平面中找到将获得所有点的半径 R1。XZ 平面 (R2) 和 YZ 平面 (R3) 也是如此。然后使用每个轴上的最大值。A=max(R1,R2), B=max(R1,R3) 和 C=max(R2,R3)。但是，首先找到所有点的平均值（中心）并将其与原点对齐。

于 2011-09-01T15:33:49.163 回答
0

我刚刚经历了同样的过程。这是一个基于 Nima Moshtagh 工作的 python 模块。在许多地方引用，但也在这个关于边界椭圆的问题中引用

该模块还处理最终椭球的绘图。享受！

https://github.com/minillinim/ellipsoid/blob/master/ellipsoid.py

于 2013-02-20T14:06:00.697 回答
0

我前段时间将 Yury Petrov 的最小二乘 Matlab fitter 移植到 Java，它只需要 JAMA：https ://github.com/mdoube/BoneJ/blob/master/src/org/doube/geometry/FitEllipsoid.java

于 2013-02-21T15:10:47.413 回答
0

这是基于随机搜索找到焦点的非常简单的方法。没有使用线性代数。因此，如果您对不完美的解决方案感到满意：

3DPoints - Array of some Amount of points
vecCenter - average of 3DPoints
AngleCosine - cos of angle between two vectors

RandomOrder(3DPoints)

vecFocus := (0, 0, 0)
for i := 0 to Amount:
    vecRadius := 3DPoints[i] - vecCenter

    // Change vecRadius direction to parallel
    if AngleCosine(vecFocus, vecRadius) < 0 then
        vecRadius *= -1
    vecFocus += (vecRadius - vecFocus) / Amount

可以通过在向后方向传递数组第二次来改进结果 Foci 放置在 vecCenter +/- vecFocus

于 2018-07-27T01:06:53.257 回答