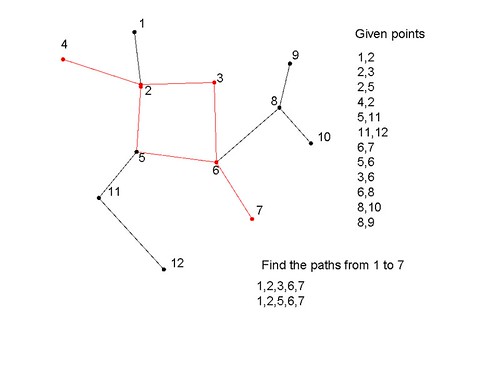
假设我有按以下方式连接的节点,我如何得出给定点之间存在的路径数量以及路径详细信息?
1,2 //node 1 and 2 are connected
2,3
2,5
4,2
5,11
11,12
6,7
5,6
3,6
6,8
8,10
8,9
找到从 1 到 7 的路径:
答案:找到 2 条路径,它们是
1,2,3,6,7
1,2,5,6,7
在这里找到的实现很好,我将使用相同的
这是python中上述链接的片段
# a sample graph
graph = {'A': ['B', 'C','E'],
'B': ['A','C', 'D'],
'C': ['D'],
'D': ['C'],
'E': ['F','D'],
'F': ['C']}
class MyQUEUE: # just an implementation of a queue
def __init__(self):
self.holder = []
def enqueue(self,val):
self.holder.append(val)
def dequeue(self):
val = None
try:
val = self.holder[0]
if len(self.holder) == 1:
self.holder = []
else:
self.holder = self.holder[1:]
except:
pass
return val
def IsEmpty(self):
result = False
if len(self.holder) == 0:
result = True
return result
path_queue = MyQUEUE() # now we make a queue
def BFS(graph,start,end,q):
temp_path = [start]
q.enqueue(temp_path)
while q.IsEmpty() == False:
tmp_path = q.dequeue()
last_node = tmp_path[len(tmp_path)-1]
print tmp_path
if last_node == end:
print "VALID_PATH : ",tmp_path
for link_node in graph[last_node]:
if link_node not in tmp_path:
#new_path = []
new_path = tmp_path + [link_node]
q.enqueue(new_path)
BFS(graph,"A","D",path_queue)
-------------results-------------------
['A']
['A', 'B']
['A', 'C']
['A', 'E']
['A', 'B', 'C']
['A', 'B', 'D']
VALID_PATH : ['A', 'B', 'D']
['A', 'C', 'D']
VALID_PATH : ['A', 'C', 'D']
['A', 'E', 'F']
['A', 'E', 'D']
VALID_PATH : ['A', 'E', 'D']
['A', 'B', 'C', 'D']
VALID_PATH : ['A', 'B', 'C', 'D']
['A', 'E', 'F', 'C']
['A', 'E', 'F', 'C', 'D']
VALID_PATH : ['A', 'E', 'F', 'C', 'D']