我有一个程序需要重复计算数据集的近似百分位数(顺序统计),以便在进一步处理之前删除异常值。我目前正在通过对值数组进行排序并选择适当的元素来做到这一点;这是可行的,但它在配置文件上是一个明显的亮点,尽管它只是该程序的一个相当小的部分。
更多信息:
- 该数据集包含多达 100000 个浮点数,并假定为“合理”分布 - 在特定值附近不太可能出现重复或密度的巨大峰值;如果由于某种奇怪的原因分布是奇怪的,那么近似值不太准确是可以的,因为数据可能无论如何都搞砸了,进一步的处理也很可疑。但是,数据不一定是均匀分布或正态分布的;它不太可能退化。
- 一个近似的解决方案会很好,但我确实需要了解近似如何引入错误以确保它是有效的。
- 由于目标是消除异常值,我一直在计算相同数据的两个百分位数:例如,一个为 95%,一个为 5%。
- 该应用程序在 C# 中,在 C++ 中进行了一些繁重的工作;伪代码或任何一个预先存在的库都可以。
- 一种完全不同的去除异常值的方法也可以,只要它是合理的。
- 更新:看来我正在寻找一个近似的选择算法。
尽管这一切都是在一个循环中完成的,但数据每次都(略有)不同,因此像对这个问题所做的那样重用数据结构并不容易。
已实施的解决方案
使用 Gronim 建议的维基百科选择算法将这部分运行时间减少了大约 20 倍。
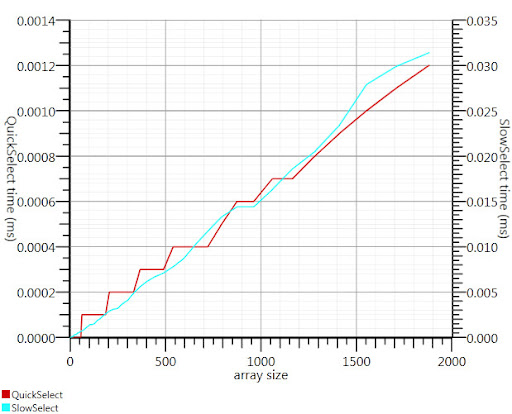
由于我找不到 C# 实现,这就是我想出的。即使对于小输入,它也比 Array.Sort 更快;在 1000 个元素时,它的速度提高了 25 倍。
public static double QuickSelect(double[] list, int k) {
return QuickSelect(list, k, 0, list.Length);
}
public static double QuickSelect(double[] list, int k, int startI, int endI) {
while (true) {
// Assume startI <= k < endI
int pivotI = (startI + endI) / 2; //arbitrary, but good if sorted
int splitI = partition(list, startI, endI, pivotI);
if (k < splitI)
endI = splitI;
else if (k > splitI)
startI = splitI + 1;
else //if (k == splitI)
return list[k];
}
//when this returns, all elements of list[i] <= list[k] iif i <= k
}
static int partition(double[] list, int startI, int endI, int pivotI) {
double pivotValue = list[pivotI];
list[pivotI] = list[startI];
list[startI] = pivotValue;
int storeI = startI + 1;//no need to store @ pivot item, it's good already.
//Invariant: startI < storeI <= endI
while (storeI < endI && list[storeI] <= pivotValue) ++storeI; //fast if sorted
//now storeI == endI || list[storeI] > pivotValue
//so elem @storeI is either irrelevant or too large.
for (int i = storeI + 1; i < endI; ++i)
if (list[i] <= pivotValue) {
list.swap_elems(i, storeI);
++storeI;
}
int newPivotI = storeI - 1;
list[startI] = list[newPivotI];
list[newPivotI] = pivotValue;
//now [startI, newPivotI] are <= to pivotValue && list[newPivotI] == pivotValue.
return newPivotI;
}
static void swap_elems(this double[] list, int i, int j) {
double tmp = list[i];
list[i] = list[j];
list[j] = tmp;
}
谢谢,Gronim,为我指明了正确的方向!