3

对于（-x 或 0）-> 无穷大的积分，我在 MATLABquadgk和 Python 的例程之间得到不一致的结果。quad我相信 MATLAB 版本是正确的（基于将flag参数从 1 切换到 -1 的感觉检查），而 Python 版本给出了错误的结果，在这种情况下为 0。MATLAB 产生 0.1022。它们是相同的integrands，我已经完成了每一步，甚至将xMATLAB 生成的值插入quadgk到 Python 中（这导致 Python 版本生成与 MATLAB 相同的值，只需将它们传递给integrand函数）。在这一点上，我希望在这里使用另一个例程而不是 SciPy，例如 Gauss-Legendre 正交https://sourceforge.net/projects/fastgausslegendrequadrature/但我不知道如何将其从 a/b 范围扩展到 -a->infinity （我见过这些方法只能达到有限数量：

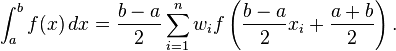https://upload.wikimedia.org/math/a/7/f/ numpy 中 Gauss-Legendre 求积的不同区间而b=np.Inf导致NaN. 也不确定如何从返回的节点和权重设置集成，虽然我一直在阅读转换但仅适用于 a 和 b 有限范围：https : //pomax.github.io/bezierinfo/legendre-gauss.html或者如果有人知道可以处理这个问题的 Python 库 - 我真的不喜欢quad没有矢量化的事实，并且可能会在 Cython 中编写代码，因为我必须快速集成 600,000 个函数（即链接到 C++ 库上面的链接）。这里真正奇怪的是，我设法通过向上移动来获得相同的结果vol在任何地方输入 >= 0.39，低于 Python 的结果在 0 处崩溃。非常令人困惑。任何帮助表示赞赏，自从微积分以来已经有好几年了......这是Python代码：

from scipy.stats import norm, lognorm
from scipy.integrate import quad
import numpy as np

def integrand(x, flag, F, K, vol, T2, T1):
    d1 = (np.log(x / (x+K)) + 0.5 * (vol**2) * (T2-T1)) / (vol * np.sqrt(T2 - T1))
    d2 = d1 - vol*np.sqrt(T2 - T1)
    mu = np.log(F) - 0.5 *vol **2 * T1
    sigma = vol * np.sqrt(T1)
    value = lognorm.pdf(x, scale=np.exp(mu), s=sigma) * (flag * x*norm.cdf(flag * d1) - flag * (x+K)*norm.cdf(flag * d2))
    return value

if __name__ == '__main__':
        flag = 1
        F = 54.31
        K = 1.1967
        vol = 0.1328
        T2 = 0.0411
        T1 = 0.0137
        quad(integrand, 0, np.Inf, args=(flag, F, K, vol, T2, T1), epsabs=1e-12)[0]

这是 MATLAB 代码（必须保存integrand为 .M，然后才能在命令窗口中输入脚本）：

function value = integrand(x, flag, F,K,vol,T2,T1)
d1 = (log(x ./ (x+K)) + 0.5 .* (vol.^2) .* (T2-T1)) ./ (vol .* sqrt(T2 - T1));
d2 = d1 - vol.*sqrt(T2 - T1);
mu = log(F) - 0.5 .*vol .^2 .* T1;
sigma = vol .* sqrt(T1);
value = lognpdf(x, mu, sigma) .* (flag .* x.*normcdf(flag .* d1) - flag .* (x+K).*normcdf(flag .* d2));
end

% 脚本部分

flag = 1
F = 54.31
K = 1.1967
vol = 0.1328
T2 = 0.0411
T1 = 0.0137
quadgk(@(x) integrand(x,flag, F, K, vol, T2, T1), 0, Inf, 'AbsTol',1e-12)

我应该注意到，当这些输入被传递时，MATLAB 和 Python 使用 quad 生成相同的结果（转置上述变量）：

 current_opt = [  -1.0000    1.2075    0.1251    0.4300    0.0685    0.0411     
                1.0000    1.2075    0.0512    0.5600    0.0685    0.0411]
4

1 回答 1

0

好吧，这很有趣。除非将epsabs变量设置得高得离谱，否则集成就会崩溃。我已经设法在 MATLAB 和 Python 之间使用epsabs=-1e1000. 尽可能慢，但至少它有效。

于 2016-05-21T18:34:57.950 回答