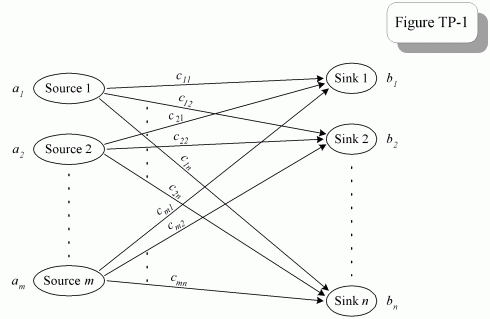
我的一位同事从在线法官网站向我提出了一个练习，该练习基本上是一个解决小镇疏散计划的图形问题。
我不需要答案（我也不想要）我只需要一个建议，因为我对这类问题有点陌生。
问题包括有工人的城镇建筑和核袭击时的辐射避难所。我必须建立一个算法，将每栋建筑物的工人分配到一个或多个辐射避难所，但在某种程度上，一些避难所不会变得过于拥挤，而其他避难所几乎是空的（否则我只会让工人去最近的一个） .
问题是这样的：http ://acm.timus.ru/problem.aspx?space=1&num=1237
到目前为止，我所做的是为每栋建筑物找到最近的庇护所，并将工人数量从该建筑物中移出，使其等于庇护所的容量。然后搬到下一栋楼。但有时工人的数量大于庇护所的容量，在这种情况下，在我遍历每座建筑物之后，我只是迭代然后再次应用相同的算法，直到每座建筑物中有 0 名工人，问题是这几乎不是最好的方法解决这个问题。
欢迎任何提示，请不要觉得我在寻求答案，我只是想要一个正确方向的建议来解决它。
提前致谢。
这看起来与转运问题完全一样，可以（显然）使用线性规划来解决。（我说得很明显，因为这看起来是整数线性规划的一个实例）。
从网站：
出现运输问题的标准场景是通过连接一组给定城市的高速公路网络发送产品单元。每个城市都被视为“源头”，因为单位将从那里运出，或者被视为“汇点”，因为那里需要单位。每个源都有给定的供应，每个汇都有给定的需求，连接源-汇对的每条高速公路都有给定的单位运输运输成本。这可以以网络的形式可视化，如下图 TP-1 所示。
给定这样一个网络，感兴趣的问题是确定一个最优的运输方案，在供需约束的情况下，使运输的总成本最小化。
希望有帮助。
这看起来像一个标准的最小成本最大流量问题。具有约 200 个顶点的二部图应该很容易及时运行。
要创建顶点约束（每个节点只能处理 k 人），您只需要创建第二个图 G_1，在其中为每个 v_i 添加一个额外的顶点 u_i - 无论您的约束是什么，都让 v_i 到 u_i 的流情况下，k+1，成本为 0。所以基本上如果原始图 G 中有一条边 (a,b)，那么在 G_1 中，每个边都会有一条边 (u_a,v_b)。实际上，您正在创建第二层顶点，将每个顶点的流限制为 k。