4

目前我正在编写一个增强现实应用程序，但在将对象显示在屏幕上时遇到了一些问题。令我非常沮丧的是，我无法将 gps 点转换为我的 android 设备上的相应屏幕点。我已经阅读了很多关于 stackoverflow 的文章和许多其他帖子（我已经问过类似的问题），但我仍然需要你的帮助。

我做了维基百科中解释的透视投影。

我与透视投影的结果有什么关系才能获得最终的屏幕点？

4

1 回答 1

15

前段时间阅读维基百科的文章时，我也很困惑。这是我尝试以不同的方式解释它：

情况

让我们简化一下情况。我们有：

  • 我们的投影点 D(x,y,z) - 你称之为relativePositionX|Y|Z
  • 大小为w * h的图像平面
  • 半视角 α

...我们想要：

  • B 在图像平面中的坐标（我们称它们为X和Y）

X 屏幕坐标的架构：

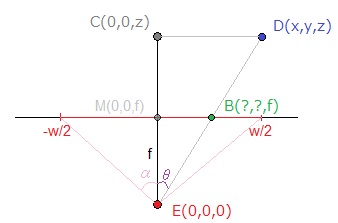
E 是我们的“眼睛”在这个配置中的位置，我选择它作为原点来简化。

已知焦距f可以估计：

  • tan(α) = (w/2) / f (1)

一点几何

您可以在图片上看到三角形ECD和EBM是相似的，因此使用Side-Splitter Theorem，我们得到：

  • MB / CD = EM / EC<=> X / x = f / z (2)

使用(1)和(2)，我们现在有：

  • X = (x / z) * ( (w / 2) / tan(α) )

如果我们回到维基百科文章中使用的符号，我们的等式相当于：

  • b_x = (d_x / d_z) * r_z

您会注意到我们缺少乘以s_x / r_x。这是因为在我们的例子中，“显示尺寸”和“记录表面”是相同的，所以s_x / r_x = 1.

注意：Y的推理相同。

实际使用

一些备注：

  • 通常使用α = 45deg，这意味着tan(α) = 1. 这就是为什么这个术语没有出现在许多实现中的原因。

  • 如果你想保持你显示的元素的比例，保持f为X和Y不变，即，而不是计算：

    • X = (x / z) * ( (w / 2) / tan(α) )和Y = (y / z) * ( (h / 2) / tan(α) )

    ... 做：

    • X = (x / z) * ( (min(w,h) / 2) / tan(α) )和Y = (y / z) * ( (min(w,h) / 2) / tan(α) )

    注意：当我说“ “显示尺寸”和“记录表面”相同”时，这并不完全正确，最小 操作是为了补偿这个近似值，使方形表面r适应潜在的-矩形表面s .

    注意 2：Appunta 没有使用min(w,h) / 2screenRatio= (getWidth()+getHeight())/2 ，而是使用你注意到的。两种解决方案都保留了元素比率。焦距以及视角会略有不同，具体取决于屏幕自身的比例。您实际上可以使用要定义的任何函数f。

  • 正如您在上图中可能已经注意到的那样，屏幕坐标在这里定义在[-w/2 ; w/2]用于 X 和[-h/2 ；h/2]表示 Y，但您可能想要 [0 ; w]和 [0 ; h]代替。X += w/2-Y += h/2问题解决了。

结论

我希望这能回答你的问题。如果需要版本，我会留在附近。

再见！

<自我宣传提醒>其实前段时间我发了一篇 关于3D投影和渲染的文章。该实现是用 Javascript 编写的，但它应该很容易翻译。

于 2013-05-23T09:13:49.333 回答