我需要一种算法来确定一个角度是否在另一个角度的一定度数内。
我的第一个想法是(a-x < b) && (a+x > b),但是当它必须使用从 -179 到 180 的角度时它会失败。
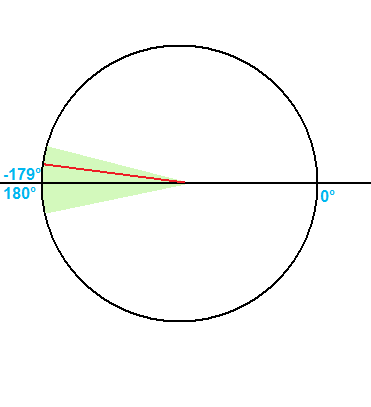
在上图中,夹角必须位于的区域(绿色)包含在负侧和正侧之间。如何确定角度(红线)是否在该区域内?
我需要一种算法来确定一个角度是否在另一个角度的一定度数内。
我的第一个想法是(a-x < b) && (a+x > b),但是当它必须使用从 -179 到 180 的角度时它会失败。

在上图中,夹角必须位于的区域(绿色)包含在负侧和正侧之间。如何确定角度(红线)是否在该区域内?
试试这个公式:
360-(|a-b|)%360<x || (|a-b|)%360<x
或者,在 PHP 中:
<?php
$b = 10;
$angle1 = -179;
$angle2 = 180;
$diff = $angle1 - $angle2;
if(abs($diff % 360) <= $b || (360-abs($diff % 360))<=$b) {
echo "yes";
} else {
echo "no";
}
?>
正如马塞尔正确指出的那样,对负数取模可能存在问题。另外,355度和5度有什么区别?它可能被计算为 350 度,但 10 度可能是人们所期望的。我们做出以下假设:
0 <= diff <= 180;2*PI;-360 < x < 360在 x 是输入角度的范围之外,并且输入:角度 a 和 b。所以算法很简单:
0 <= x < 360;第一步,要将角度转换为所需范围,有两种可能性:
x >= 0: 正常 = x % 360x < 0: 正常 = (-x / 360 + 1) * 360 + x第二个旨在消除对负模运算的解释差异的任何歧义。因此,举一个 x = -400 的工作示例:
-x / 360 + 1
= -(-400) / 360 + 1
= 400 / 360 + 1
= 1 + 1
= 2
然后
normal = 2 * 360 + (-400)
= 320
因此对于输入 10 和 -400,法线角度为 10 和 320。
现在我们计算它们之间的最短角度。作为一个健全的检查,这两个角度的总和必须是 360。在这种情况下,可能性是 50 和 310(画出来,你会看到这个)。要解决这些问题:
normal1 = min(normal(a), normal(b))
normal2 = max(normal(a), normal(b))
angle1 = normal2 - normal1
angle2 = 360 + normal1 - normal2
所以对于我们的例子:
normal1 = min(320, 10) = 10
normal2 = max(320, 10) = 320
angle1 = normal2 - normal1 = 320 - 10 = 310
angle2 = 360 + normal1 - normal2 = 360 + 10 - 320 = 50
你会注意到normal1 + normal2 = 360(如果你愿意,你甚至可以证明会是这种情况)。
最后:
diff = min(normal1, normal2)
或者在我们的例子中是 50。
您还可以使用点积:
cos(a)*cos(b) + sin(a)*sin(b) >= cos(x)
对于半径 1,线端点之间的距离是 2sin((ab/2)。所以扔掉 2,因为您只对比较感兴趣,并将 sin(x/2) 与 sin((ab)/ 进行比较2). trig 函数负责所有的包装。
c++ 实现:
float diff = fabsf(angle1 - angle2);
bool isInRange = fmodf(diff, 360.0f) <= ANGLE_RANGE ||
360.0f - fmodf(diff, 360.0f) <= ANGLE_RANGE;