c# - 在 C# 中将 π 计算为“无限”二进制精度

Question

到目前为止，Fabrice Bellard 的 base 2 方程似乎是可行的方法

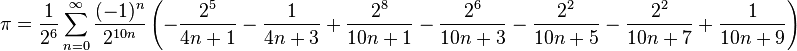
具有讽刺意味的是，这将需要一个 BigReal 类型；我们有这个 .Net 吗？.Net 4.0 有 BigInteger。

有人有Haskell版本吗？

Answer 1

由于您要的是 Haskell 版本，这里是Jerzy Karczmarczuk 的一篇论文，名为“世界上最不可靠的计算 π 的技术”：

这篇论文是惰性函数式编码中的非典型练习，是为了娱乐和指导而编写的。任何了解编程语言 Haskell 的人都可以阅读和理解它。我们展示了如何以共同递归的增量方式实现 π 的 Bailey-Borwein-Ploue 公式，从而产生数字 3、1、4、1、5、9。. 直到内存耗尽。如果有人需要很多数字，这不是一种方法！我们的编码策略是不正当和危险的，而且它被证明是失败的。它基于表示以整数为基数扩展的真分数的无限数字序列域上的算术。我们展示了如何操作：加法、乘以一个整数等。这样的序列从左到右无止境，由于模棱两可，这显然不能在所有情况下都有效。结论中讨论了一些深刻的哲学后果。

它并没有真正以有效或非常实用的方式解决问题，但很有趣并显示了惰性无限精度算术的一些问题。

还有Jeremy Gibbons 的这篇论文。

Answer 2

到目前为止，我最喜欢的 Haskell pigot 来自 Jeremy Gibbons：

pi = g(1,0,1,1,3,3) where
    g(q,r,t,k,n,l) = 
        if 4*q+r-t<n*t
        then n : g(10*q,10*(r-n*t),t,k,div(10*(3*q+r))t-10*n,l)
        else g(q*k,(2*q+r)*l,t*l,k+1,div(q*(7*k+2)+r*l)(t*l),l+2)

证明实施的数学背景可以在以下方面找到：

Pi 数字的 Spigot 算法

Answer 3

Wikipedia 详细介绍了许多获取 pi 数值近似值的方法。他们还提供了一些示例伪代码

编辑：如果你对这类数学问题感兴趣，但没有任何相关的现实问题需要解决（这绝对是一个很好的态度，恕我直言），你可以访问欧拉项目页面

Answer 4

在基于DLR的动态语言（例如IronPython）中存在处理大有理数的可能性。或者，您可以通过P/Invoke使用任何可移植的 C/C++ 大实数实现。