我对计算中的无限数很好奇，尤其是 pi。
对于要渲染圆的计算机，它必须了解 pi。但如果它是无限的，它怎么可能呢？
我是不是看得太多了？它会只使用四舍五入的值吗？
问问题
1496 次
10 回答
15
在数学上，计算机既是有限的又是非连续的，因此既不能完全知道 PI，也不能正确地绘制圆。
然而，在数字领域中，这些都不存在，因此近似 PI 然后使用它来近似渲染圆就足够了，从而产生与从精确 PI 计算得到的完全相同的像素。
无论哪种方式，生成的像素也不是真正的圆，因为它们是数字点的有限集合，而圆是由无限数量的点组成的曲线，大多数点具有无理值。
（有人向我指出，PI 通常不用于绘制圆，这是事实，但是，用于绘制圆的方法与用于表示和/或计算 PI 值的公式有关，其中仍然有同样的问题）。
于 2009-07-27T22:16:17.560 回答
7
一个近似值通常就足够了。要“渲染”一个圆圈，计算机只需要充分理解 pi 即可在所需的任何分辨率（有限）下准确地渲染。
编辑：正如其他人指出的那样，你甚至不需要 pi 来渲染一个圆圈。不过，问题的要点是“计算机如何处理像 pi 这样的数字？” 他们使用近似值，而使用这些近似值的人必须确定它们对于给定目的是否足够精确。
于 2009-07-27T22:06:48.203 回答
6
你根本不需要 PI 来画一个圆圈。画圆的方法有很多种。天真的方法是使用正弦和余弦。
我在 8 位机器上最常看到的算法是Bresenham 的循环。你甚至不需要浮点数学。
于 2009-07-27T22:35:20.953 回答
2
编程语言对 pi 和类似的“无限”数使用四舍五入的常数。
为了获得更高的精度，您可以使用迭代算法，只要需要，就可以循环使用。
于 2009-07-27T22:26:30.347 回答
2
在某处我看到了一个证据，证明要在宇宙周围画一个精确到毫米精度的圆，你需要少于 100 位的 pi，换句话说，比手上有太多时间的人计算的数字要少得多（或计算能力太强...）。现在，要是我能找到那个证据就好了……（编辑）找到了
于 2009-07-28T01:27:02.067 回答
2
计算机只是使用 pi 的一个很好的近似值。
来自 MSDN 关于System.Math.PI的文章
该字段的值为 3.14159265358979323846。
顺便说一句：PI 不是无限的。它是非理性的，这意味着它有无数个不重复的小数位。PI 有几个非常短的表达式。（有关更多详细信息，请参阅维基百科页面）
这是 PI 的一个非常简短的表达式：
于 2009-07-27T22:06:58.623 回答
1
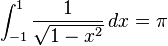
Pi不是无限的，它是非理性的，这意味着您不能将其表示为商。它有无限位数。 http://en.wikipedia.org/wiki/Proof_that_π_is_irrational
关于计算在这里找到一些信息。 http://en.wikipedia.org/wiki/Computing_π
不错的页面也是这个 http://3.141592653589793238462643383279502884197169399375105820974944592.com/
于 2009-07-27T22:46:20.777 回答
1
我相信它将它四舍五入到一个非常小的数字，并且很可能是一个常数。如果您使用 PHP，这是 PI 呈现的方式：
回声 pi(); // 3.1415926535898 回声 M_PI; // 3.1415926535898
就像你在高中只需要 3.14159 一样，计算机只需要这么多就可以让它相当准确。
于 2009-07-27T22:08:05.283 回答
1
计算机只使用四舍五入的 pi 值，当然除非有特殊情况，例如科学计算。例如，在 python 中 pi 表示为：
>>> import math
>>> math.pi
3.1415926535897931
你可以在 IDLE，pythons 交互式解释器中自己测试一下。
于 2009-07-27T22:08:50.790 回答