20

如何判断一个点是否属于某条线？

如果可能的话，我们会赞赏示例。

4

10 回答 10

30

在最简单的形式中，只需将坐标插入直线方程并检查是否相等。

鉴于：

Point p (X=4, Y=5)
Line l (Slope=1, YIntersect=1)

插入 X 和 Y：

   Y = Slope * X + YIntersect
=> 5 = 1 * 4 + 1
=> 5 = 5

所以，是的，重点就在眼前。

如果您的线以 (X1,Y1),(X2,Y2) 形式表示，那么您可以计算斜率：

 Slope = (y1 - y2) / (x1-x2)

然后用这个得到 Y-Intersect：

 YIntersect = - Slope * X1 + Y1;

编辑：我修复了 Y 相交（一直是 X1 / Y1 ...）

你必须检查那x1 - x2不是0。如果是，那么检查该点是否在线是一个简单的问题，即检查您的点中的 Y 值是否等于x1或x2。此外，请检查该点的 X 是否不是“x1”或“x2”。

于 2009-05-25T17:02:54.973 回答
26

我刚刚编写了一个函数来处理一些额外的要求，因为我在绘图应用程序中使用了这个检查：

  • 模糊性 - 由于该功能用于通过单击来选择行，因此必须有一些错误空间。
  • 这条线有一个 EndPoint 和一个 StartPoint，没有无限的线。
  • 必须处理垂直和水平直线， (x2 - x1) == 0 导致在其他答案中除以零。
private const double SELECTION_FUZZINESS = 3;

internal override bool ContainsPoint(Point point)
{
    LineGeometry lineGeo = geometry as LineGeometry;
    Point leftPoint;
    Point rightPoint;

    // Normalize start/end to left right to make the offset calc simpler.
    if (lineGeo.StartPoint.X <= lineGeo.EndPoint.X)
    {
        leftPoint   = lineGeo.StartPoint;
        rightPoint  = lineGeo.EndPoint;
    }
    else
    {
        leftPoint   = lineGeo.EndPoint;
        rightPoint  = lineGeo.StartPoint;
    }

    // If point is out of bounds, no need to do further checks.                  
    if (point.X + SELECTION_FUZZINESS < leftPoint.X || rightPoint.X < point.X - SELECTION_FUZZINESS)
        return false;
    else if (point.Y + SELECTION_FUZZINESS < Math.Min(leftPoint.Y, rightPoint.Y) || Math.Max(leftPoint.Y, rightPoint.Y) < point.Y - SELECTION_FUZZINESS)
        return false;

    double deltaX = rightPoint.X - leftPoint.X;
    double deltaY = rightPoint.Y - leftPoint.Y;

    // If the line is straight, the earlier boundary check is enough to determine that the point is on the line.
    // Also prevents division by zero exceptions.
    if (deltaX == 0 || deltaY == 0) 
        return true;

    double slope        = deltaY / deltaX;
    double offset       = leftPoint.Y - leftPoint.X * slope;
    double calculatedY  = point.X * slope + offset;

    // Check calculated Y matches the points Y coord with some easing.
    bool lineContains = point.Y - SELECTION_FUZZINESS <= calculatedY && calculatedY <= point.Y + SELECTION_FUZZINESS;

    return lineContains;            
}
于 2012-12-06T10:37:50.860 回答
21

确定点 R = (rx, ry) 是否位于连接点 P = (px, py) 和 Q = (qx, qy) 的线上的最佳方法是检查矩阵的行列式是否

{{qx - px, qy - py}, {rx - px, ry - py}},

即 (qx - px) * (ry - py) - (qy - py) * (rx - px) 接近于 0。与发布的其他解决方案相比，此解决方案具有几个相关优势：首先，它不需要垂直线的特殊情况，第二，它不会除法（通常是一个缓慢的操作），第三，当线条几乎但不是完全垂直时，它不会触发不良的浮点行为。

于 2009-05-25T17:31:34.283 回答
7

给定线上的两个点L0和L1要测试的点P。

               (L1 - L0) * (P - L0)
n = (P - L0) - --------------------- (L1 - L0)
               (L1 - L0) * (L1 - L0)

向量的范数n是点P到通过L0和的线的距离L1。如果此距离为零或足够小（在舍入误差的情况下），则该点位于线上。

符号*代表点积。

例子

P = (5, 5)

L0 = (0, 10)
L1 = (20, -10)

L1 - L0 = (20, -20)
P  - L0 = (5, -5)

              (20, -20) * (5, -5)
n = (5, -5) - --------------------- (20, -20)
              (20, -20) * (20, -20)

              200
  = (5, -5) - --- (20, -20)
              800

  = (5, -5) - (5, -5)

  = (0, 0)
于 2009-05-25T17:17:24.767 回答
6

我认为Patrick McDonald 先生给出了几乎正确的答案，这是对他答案的更正：

public bool IsOnLine(Point endPoint1, Point endPoint2, Point checkPoint)
{
    return (((double)checkPoint.Y - endPoint1.Y)) / ((double)(checkPoint.X - endPoint1.X))
        == ((double)(endPoint2.Y - endPoint1.Y)) / ((double)(endPoint2.X - endPoint1.X));
}

当然还有很多其他的正确答案，尤其是 Mr.Josh，但我发现这是最好的答案。

谢谢大家。

于 2009-05-25T18:07:51.933 回答
4 
y = m * x + c

这是一条线的方程。x & y 是坐标。每条线的特征在于它的斜率 (m) 以及它与 y 轴 (c) 相交的位置。

因此，给定一条线的 m & c，您可以通过检查等式是否适用于 x = x1 和 y = y1 来确定点 (x1, y1) 是否在线上

于 2009-05-25T17:00:36.113 回答
3

二维线通常使用两个变量 x 和 y 的方程来表示，这里是一个众所周知的方程

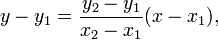
y-y1 = (y1-y2)/(x1-x2) (x-x1)

现在想象您的 GDI+ 线是从 (0,0) 到 (100, 100) 绘制的，然后 m=(0-100)/(0-100) = 1 的值因此您的线的等式是 y-0=1 *(x-0) => y=x

既然我们有一个关于这条线的方程，那么很容易测试一个点是否属于这条线。当您替换 x=x3 和 y=y3 时，如果给定点 (x3, y3) 满足直线方程，则它属于该直线。例如，点 (10, 10) 属于这条线，因为 10=10，但 (10,12) 不属于这条线，因为 12 != 10。

注意：对于垂直线，斜率 (m) 的值是无限的，但对于这种特殊情况，您可以直接使用垂直线的方程 x=c，其中 c = x1 = x2。

虽然我不得不说我不确定这是否是最有效的方法。当我手头有更多时间时，我会尝试找到更有效的方法。

希望这可以帮助。

于 2009-05-25T17:11:51.280 回答
3

如果您有一条由其端点定义的线

PointF pt1, pt2;

你有一点要检查

PointF checkPoint;

那么你可以定义一个函数如下：

bool IsOnLine(PointF endPoint1, PointF endPoint2, PointF checkPoint) 
{
    return (checkPoint.Y - endPoint1.Y) / (endPoint2.Y - endPoint1.Y)
        == (checkPoint.X - endPoint1.X) / (endPoint2.X - endPoint1.X);
}

并按如下方式调用它：

if (IsOnLine(pt1, pt2, checkPoint) {
    // Is on line
}

不过，您将需要检查除以零。

于 2009-05-25T17:15:59.043 回答
1

直线方程为：

y = mx + c

所以一个点（a，b）在这条线上，如果它满足这个方程，即b = ma + c

于 2009-05-25T17:06:08.510 回答
0

作为该方法的替代slope/y-intercept方法，我使用以下方法选择了这种方法Math.Atan2：

// as an extension method
public static bool Intersects(this Vector2 v, LineSegment s) {
    //  check from line segment start perspective
    var reference = Math.Atan2(s.Start.Y - s.End.Y, s.Start.X - s.End.X);
    var aTanTest = Math.Atan2(s.Start.Y - v.Y, s.Start.X - v.X);

    //  check from line segment end perspective
    if (reference == aTanTest) {
        reference = Math.Atan2(s.End.Y - s.Start.Y, s.End.X - s.Start.X);
        aTanTest = Math.Atan2(s.End.Y - v.Y, s.End.X - v.X);
    }

    return reference == aTanTest;
}

第一次检查reference确定从线段起点到终点的 arcTan。然后从起点角度，我们确定arcTan到vector v。

如果这些值相等，我们从端点的角度进行检查。

简单并处理水平、垂直和介于两者之间的所有其他内容。

于 2016-04-01T20:31:06.307 回答