8

感觉就像我被困住了，我的朋友们。有人可以解释我从“功能算法设计的珍珠”第 11 章（“不是最大段总和”）中挑选方程。

这是问题（有点简化）让我们有一些具有给定转换的状态：

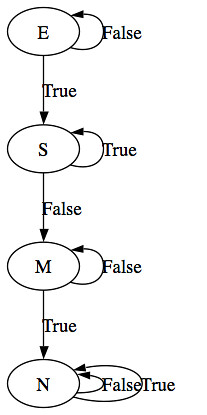
data State = E | S | M | N 
                deriving (Show, Eq) 

step E False = E 
step E True = S 
step S False = M 
step S True = S 
step M False = M 
step M True = N 
step N False = N 
step N True = N

现在，让我们定义pick：

 pick q = map snd . filter ((== q) . fst) . map (\a -> (foldl step E a, a))

作者声称以下七个等式成立：

pick E xs = [[]]
pick S [ ] = [ ]
pick S (xs ++ [x]) = map (++[x ]) (pick S xs ++ pick E xs)
pick M [ ] = [ ]
pick M (xs ++ [x ]) = pick M xs ++ pick S xs
pick N [ ] = [ ]
pick N (xs ++ [x]) = pick N xs ++ map (++[x]) (pick N xs ++ pick M xs)

有人可以用简单的话解释我，为什么这些方程式是正确的，我们如何证明一个明显的证据？我觉得我几乎理解了 S 方程，但总的来说这仍然是难以捉摸的。

4

1 回答 1

18

好的，我需要可视化您的状态图：

q7967337

并为pick :: State -> [[Bool]] -> [(State, [Bool]).

现在，这与您的第一个方程式不符pick E xs = [[]]- 它必须是pick E xs = [(E,[])].

也许您打算这样定义pick：

pick :: State -> [[Bool]] -> [[Bool]]
pick q = map snd . filter ((== q) . fst) . map (\a -> (foldl step E a, a))

假设这个定义，第一个等式现在是有意义的。它声称，如果您从 开始E，那么唯一的布尔值序列xs将以E空列表结束。

请注意，这假设[]∈ xs。

此外，如果ys = replicate n False, pick E [ys] = [ys], 所以这意味着 ∀ n, ys∉ xs。

第二个、第四个和第六个方程都是 的形式，根据和pick _ [ ] = [ ]的定义，这很简单。mapfilter

第三个等式pick S (xs ++ [x]) = map (++[x ]) (pick S xs ++ pick E xs)也没有任何意义。我猜它想说的是：

pick S (map (++[True] xs) = map (++[True]) (pick S xs ++ pick E xs)

也就是说 - 任何开始E和结束于的路径S都可以通过采用现有路径来构建EorS并附加True。等效地，每条以 结尾的路径都S必须以True.

第五个等式同样荒谬，应表述为：

pick S (map (++[False] xs) = map (++[False]) (pick S xs ++ pick M xs)

第七个等式应重述为：

pick N (map (++ [True]) xs) = pick N xs ++ map (++[True]) (pick N xs ++ pick M xs)
于 2011-11-01T14:29:41.917 回答