1

如果以错误的方式使用它，我很抱歉在 StackOverflow 上提问。

我在一篇论文中有一个最大化问题，就像这样：

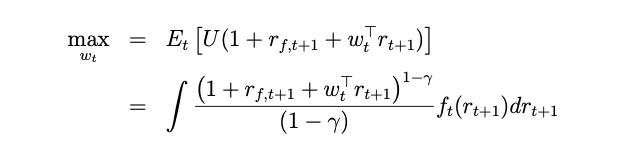
CRRA.png

和一些限制：

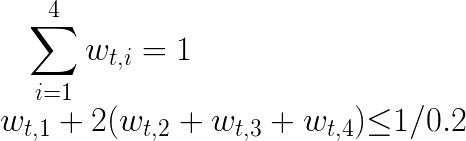
CodeCogsEqn.png

其中r_f,t+1和γ给定常数，r_t+1是多维随机变量向量（这里是4维），f_t(r_t+1)是r_t+1的多维分布函数。问题是找到一个权重向量 w_t 来最大化期望值。

该论文说它是如何解决这个问题的，“积分是通过从多元条件回报分布 f_t(rt+1) 模拟 4 个因子（r_t+1 向量）的 100,000 个变量来解决的”。我知道如何生成随机数并从分布中获取平均值，但不完全了解如何在优化问题中使用它。

我尝试使用一些随机数并将平均值作为目标函数返回，如下例所示：

import numpy as np
rands = np.random.multivariate_normal(mean=[0, 0, 0, 0],
                                      cov=[[1, 0, 0, 0], [0, 1, 0, 0],
                                           [0, 0, 1, 0], [0, 0, 0, 1]],
                                      size=1000)


def expect_value(weight, rf, gamma, fac_ndarr):
    weight = np.asarray(weight)
    utility_array = (1 + rf + fac_ndarr.dot(weight))**(1 - gamma) / (1 - gamma)

    expected_value = utility_array.mean()
    return -expected_value

接下来，我使用模块mystic来解决全局最小值。

from mystic.solvers import diffev2
from mystic.symbolic import (generate_conditions, generate_penalty,
                             generate_constraint, generate_solvers, simplify)

equation = """
x0 + x1 + x2 + x3 == 1
x0 + 2*(x1 + x2 + x3) - (1. / 0.2) <= 0
"""

pf = generate_penalty(generate_conditions(equation), k=1e20)
cf = generate_constraint(generate_solvers(simplify(equation)))
bounds = [(0, 1)] * 4

# Here the given constant `rf` and `gamma` are 0.15 and 7, 
# and they were passed to the parameter `args` with `rands`, 
# the `args` will be passed to the `cost`funtion.
result = diffev2(cost=expect_value,
                 args=(0.15, 7, rands),
                 x0=bounds,
                 bounds=bounds,
                 constraint=cf,
                 penalty=pf,
                 full_output=True,
                 npop=40)

我真正的问题产生了 50000 个随机数，似乎找不到确切的全局最小解，因为每次代码找到不同的解并且目标函数的值不同。即使在阅读文档并将参数“npop”更改为 1000 并将“scale”（试验解决方案的突变乘数）更改为 0.1 之后，它也没有按预期工作。

我用来解决优化问题的方式是不是错了？使用模拟数据最大化期望值的确切方法是什么？还是使用神秘模块有什么问题？或者，是否有另一种有效的方法来解决上述最大化问题？

非常感谢您的帮助！</p>

4

1 回答 1

0

mystic 是为这种确切类型的问题而构建的，因为它可以在产品测量空间中进行优化。见：https ://github.com/uqfoundation/mystic/blob/master/examples5/TEST_OUQ_surrogate_diam.py

于 2019-12-02T20:30:54.443 回答