22

在 Stack Overflow 播客 #36 ( https://blog.stackoverflow.com/2009/01/podcast-36/ ) 中，表达了这种观点：一旦您了解设置状态机是多么容易，您就会永远不要再尝试不恰当地使用正则表达式。

我做了一堆搜索。我找到了一些学术论文和其他复杂的例子，但我想找到一个简单的例子来帮助我理解这个过程。我使用了很多正则表达式，并且我想确保我永远不会再“不恰当地”使用一个。

4

6 回答 6

27

当然，尽管您需要更复杂的示例才能真正理解 RE 的工作原理。考虑以下 RE：

^[A-Za-z][A-Za-z0-9_]*$

这是一个典型的标识符（必须以 alpha 开头，并且可以有任意数量的字母数字和取消划线字符，包括没有）。以下伪代码显示了如何使用有限状态机完成此操作：

state = FIRSTCHAR
for char in all_chars_in(string):
    if state == FIRSTCHAR:
            if char is not in the set "A-Z" or "a-z":
                error "Invalid first character"
            state = SUBSEQUENTCHARS
            next char
    if state == SUBSEQUENTCHARS:
            if char is not in the set "A-Z" or "a-z" or "0-9" or "_":
                error "Invalid subsequent character"
            state = SUBSEQUENTCHARS
            next char

现在，正如我所说，这是一个非常简单的例子。它没有展示如何进行贪婪/非贪婪匹配、回溯、一行内（而不是整行）匹配以及状态机的其他更深奥的特性，这些特性很容易被 RE 语法处理。

这就是 RE 如此强大的原因。执行单行 RE 可以执行的操作所需的实际有限状态机代码通常非常长且复杂。

您可以做的最好的事情是获取特定简单语言的一些 lex/yacc（或等效）代码的副本，然后查看它生成的代码。它不漂亮（它不一定是因为它不应该被人类阅读，他们应该查看 lex/yacc 代码）但它可能会让你更好地了解它们是如何工作的。

于 2009-02-08T02:36:43.613 回答
26

在任何模式上使用 python 鲜为人知的 re.DEBUG 标志的一种相当方便的方法来帮助查看这一点：

>>> re.compile(r'<([A-Z][A-Z0-9]*)\b[^>]*>(.*?)</\1>', re.DEBUG)
literal 60
subpattern 1
  in
    range (65, 90)
  max_repeat 0 65535
    in
      range (65, 90)
      range (48, 57)
at at_boundary
max_repeat 0 65535
  not_literal 62
literal 62
subpattern 2
  min_repeat 0 65535
    any None
literal 60
literal 47
groupref 1
literal 62

'literal' 和 'range' 后面的数字是指它们应该匹配的 ascii 字符的整数值。

于 2009-02-08T03:01:01.723 回答
20

让你自己在飞行中！

http://osteele.com/tools/reanimator/???

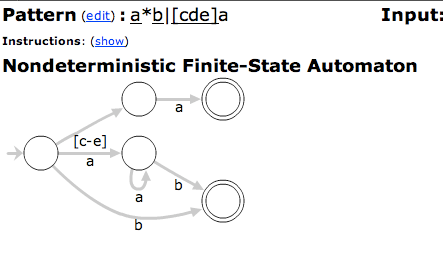
有限状态机

这是一个非常好的组合工具，可以将正则表达式可视化为 FSM。它不支持您在现实世界的正则表达式引擎中找到的某些语法，但肯定足以准确理解正在发生的事情。

于 2009-02-08T02:46:18.227 回答
4

问题是“我如何选择状态和转换条件？”还是“我如何在 Foo 中实现我的抽象状态机？”

如何选择状态和转换条件？

我通常将 FSM 用于相当简单的问题并直观地选择它们。在我对关于正则表达式的另一个问题的回答中，我只是将解析问题视为其中之一Inside或outside标记对，并从那里写出转换（具有开始和结束状态以保持实现干净）。

如何在 Foo 中实现我的抽象状态机？

如果您的实现语言支持像c'switch语句这样的结构，那么您打开当前状态并处理输入以查看接下来执行的操作和/或转换。

如果没有switch-like 结构，或者如果它们在某些方面存在缺陷，则可以设置if分支样式。啊。

在我链接的示例中全部写在一个地方c看起来像这样：

token_t token;
state_t state=BEGIN_STATE;
do {
   switch ( state.getValue() ) {
   case BEGIN_STATE;
      state=OUT_STATE;
      break;
   case OUT_STATE:
      switch ( token.getValue() ) {
         case CODE_TOKEN:
            state = IN_STATE;
            output(token.string());
            break;
         case NEWLINE_TOKEN;
            output("<break>");
            output(token.string());
            break;
         ...
      }
      break;
   ...
   }
} while (state != END_STATE);

这非常混乱，所以我通常将这些state案例撕成单独的功能。

于 2009-02-08T02:49:36.253 回答
2

我敢肯定有人有更好的例子，但你可以查看 Phil Haack 的这篇文章，它有一个正则表达式的例子和一个做同样事情的状态机（之前的一篇文章也有几个正则表达式的例子我认为..）

检查该页面上的“HenriFormatter”。

于 2009-02-08T02:18:00.530 回答
1

我不知道您已经阅读了哪些学术论文，但理解如何实现有限状态机确实并不难。有一些有趣的数学，但想法实际上很容易理解。理解 FSM 最简单的方法是通过输入和输出（实际上，这包含了大部分正式定义，我不会在这里描述）。“状态”本质上只是描述一组已经发生并且可以从某个点发生的输入和输出。

有限状态机通过图表最容易理解。例如：

替代文字 http://img6.imageshack.us/img6/7571/mathfinitestatemachinedco3.gif

这就是说，如果您从某个状态 q0（旁边带有 Start 符号的状态）开始，您可以转到其他状态。每个状态都是一个圆圈。每个箭头代表一个输入或输出（取决于您如何看待它）。考虑有限状态机的另一种方法是根据“有效”或“可接受”输入。某些输出字符串不可能是某些有限状态机；这将允许您“匹配”表达式。

现在假设您从 q0 开始。现在，如果您输入 0，您将进入状态 q1。但是，如果您输入 1，您将进入状态 q2。您可以通过输入/输出箭头上方的符号看到这一点。

假设您从 q0 开始并获得此输入

0, 1, 0, 1, 1, 1

这意味着你已经经历了状态（没有输入 q0，你只是从那里开始）：

q0 -> q1 -> q0 -> q1 -> q0 -> q2 -> q3 -> q3

如果没有意义，请用手指跟踪图片。请注意，对于输入 0 和 1，q3 会返回到自身。

另一种说法是“如果您处于状态 q0 并且您看到 0 转到 q1，但如果您看到 1 转到 q2。” 如果您为每个状态都设置了这些条件，那么您几乎完成了对状态机的定义。您所要做的就是拥有一个状态变量，然后是一种输入输入的方法，基本上就是这样。

好的，那么为什么这对于乔尔的声明很重要？好吧，建立“一个真正的正则表达式来统治他们所有人”可能非常困难，也很难维护修改，甚至很难让其他人回来理解。此外，在某些情况下它更有效。

当然，状态机还有许多其他用途。希望这在一些小方面有所帮助。请注意，我没有费心深入理论，但有一些关于 FSM 的有趣证明。

于 2009-02-08T02:43:52.600 回答