0

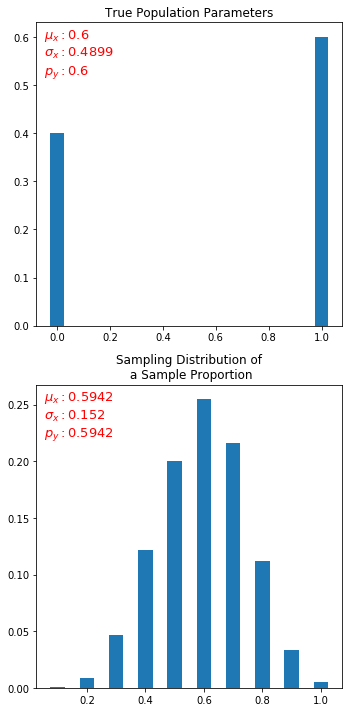
我试图使用 Python 模拟“样本比例的抽样分布”。我尝试使用伯努利变量，如示例here

关键是，在大量的口香糖中，我们有真正比例为0.6的黄色球。如果我们抽取样本（一些大小，比如 10 个），取其平均值并绘图，我们应该得到一个正态分布。

我试图在 python 中做，但我总是得到均匀分布（或在中间平坦）。我无法理解我错过了什么。

程序：

from SDSP import create_bernoulli_population, get_frequency_df
from random import shuffle, choices
from bi_to_nor_demo import get_metrics, bare_minimal_plot
import matplotlib.pyplot as plt


N = 10000  # 10000 balls
p = 0.6    # probability of yellow ball is 0.6, and others (1-0.6)=>0.4
n_pickups = 1000       # sample size
n_experiments = 100  # I dont know what this is called 


# generate population
population = create_bernoulli_population(N,p)
theor_df = get_frequency_df(population)
theor_df

# choose sample, take mean and add to X_mean_list. Do this for n_experiments times
X_hat = []
X_mean_list = []
for each_experiment in range(n_experiments):
    X_hat = choices(population, k=n_pickups)  # this method is with replacement
    shuffle(population)
    X_mean = sum(X_hat)/len(X_hat)
    X_mean_list.append(X_mean)

# plot X_mean_list as bar graph
stats_df = get_frequency_df(X_mean_list)
fig, ax = plt.subplots(1,1, figsize=(5,5))
X = stats_df['x'].tolist()
P = stats_df['p(x)'].tolist()    
ax.bar(X, P, color="C0") 

plt.show()

依赖函数：
bi_to_nor_demo
SDSP

输出：
在此处输入图像描述

更新： 我什至尝试了如下统一分布，但得到了类似的输出。不收敛到正常:(。（使用下面的函数代替 create_bernoulli_population）

def create_uniform_population(N, Y=[]):
    """
    Given the total size of population N, 
    this function generates list of those outcomes uniformly distributed
    population list
    N - Population size, eg N=10000
    p - probability of interested outcome  
    Returns the outcomes spread out in population as a list
    """
    uniform_p = 1/len(Y)
    print(uniform_p)
    total_pops = []
    for i in range(0,len(Y)):
        each_o = [i]*(int(uniform_p*N))
        total_pops += each_o
    shuffle(total_pops)    
    return total_pops
4

3 回答 3

1

你能分享你的matplotlib设置吗？我认为你的情节被截断了，你是正确的，因为伯努利样本比例的样本分布应该正态分布在总体预期值周围......

也许使用一些东西：

plt.tight_layout()

检查是否没有图表问题

于 2018-08-07T11:04:32.223 回答
1 
def plotHist(nr, N, n_):
    ''' plots the RVs'''
    x = np.zeros((N))
    sp = f.add_subplot(3, 2, n_ )

    for i in range(N):    
        for j in range(nr):
            x[i] += np.random.binomial(10, 0.6)/10 
        x[i] *= 1/nr
    plt.hist(x, 100, normed=True, color='#348ABD', label=" %d RVs"%(nr));
    plt.setp(sp.get_yticklabels(), visible=False)


N = 1000000   # number of samples taken
nr = ([1, 2, 4, 8, 16, 32])

for i in range(np.size(nr)):
    plotHist(nr[i], N, i+1)

以上是基于我在 CLT 上写的一般博客的代码示例：https ://rajeshrinet.github.io/blog/2014/central-limit-theorem/

本质上，我从 (0,1) 范围内的分布中生成几个随机数 (nr) 并将它们相加。然后我看到，当我增加随机数的数量时，它们是如何收敛的。

这是代码和结果的屏幕截图。

于 2018-08-07T11:28:17.623 回答
0

解决方案：
我想我已经找到了解决方案。通过对 Rajesh 的方法进行逆向工程并从 Daniel 那里得到提示，如果图形可能是一个问题，我终于找到了罪魁祸首：默认条形图宽度为 0.8 太宽，无法将我的图形显示为顶部扁平。下面是修改后的代码和输出。 

from SDSP import create_bernoulli_population, get_frequency_df
from random import shuffle, choices
from bi_to_nor_demo import get_metrics, bare_minimal_plot
import matplotlib.pyplot as plt

N = 10000  # 10000 balls
p = 0.6    # probability of yellow ball is 0.6, and others (1-0.6)=>0.4
n_pickups = 10       # sample size
n_experiments = 2000  # I dont know what this is called 


# THEORETICAL PDF
# generate population and calculate theoretical bernoulli pdf
population = create_bernoulli_population(N,p)
theor_df = get_frequency_df(population)


# STATISTICAL PDF
# choose sample, take mean and add to X_mean_list. Do this for n_experiments times. 
X_hat = []
X_mean_list = []
for each_experiment in range(n_experiments):
    X_hat = choices(population, k=n_pickups)  # choose, say 10 samples from population (with replacement)
    X_mean = sum(X_hat)/len(X_hat)
    X_mean_list.append(X_mean)
stats_df = get_frequency_df(X_mean_list)


# plot both theoretical and statistical outcomes
fig, (ax1,ax2) = plt.subplots(2,1, figsize=(5,10))
from SDSP import plot_pdf
mu,var,sigma = get_metrics(theor_df)
plot_pdf(theor_df, ax1, mu, sigma, p, title='True Population Parameters')
mu,var,sigma = get_metrics(stats_df)
plot_pdf(stats_df, ax2, mu, sigma, p=mu, bar_width=round(0.5/n_pickups,3),title='Sampling Distribution of\n a Sample Proportion')
plt.tight_layout()
plt.show()

输出：
output_solved

于 2018-08-07T16:33:43.213 回答