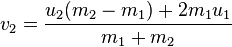graphics - 球对球碰撞 - 检测和处理

Question

在 Stack Overflow 社区的帮助下，我编写了一个非常基本但有趣的物理模拟器。

替代文字

您单击并拖动鼠标来发射一个球。它会反弹并最终停在“地板”上。

我要添加的下一个重要功能是球对球碰撞。球的运动被分解为 ax 和 y 速度矢量。我有重力（每一步 y 向量的小减少），我有摩擦（每次与墙壁碰撞时两个向量的小减少）。球以令人惊讶的逼真方式诚实地移动。

我想我的问题有两个部分：

检测球对球碰撞的最佳方法是什么？
我是否只有一个 O(n^2) 循环遍历每个球并检查每个其他球以查看其半径是否重叠？
我用什么方程来处理球对球的碰撞？物理 101
它如何影响两个球的速度 x/y 向量？两个球朝哪个方向飞去？我如何将其应用于每个球？

替代文字

处理“墙壁”的碰撞检测和由此产生的矢量变化很容易，但我看到球碰撞更复杂。对于墙壁，我只需要取适当的 x 或 y 向量的负值，然后它就会朝着正确的方向前进。对于球，我不认为是那样的。

一些快速澄清：为简单起见，我现在可以完全弹性碰撞，而且我所有的球现在都具有相同的质量，但我将来可能会改变它。

编辑：我发现有用的资源

带有向量的 2d Ball 物理：2-Dimensional Collisions without Trigonometry.pdf
2d Ball 碰撞检测示例：添加碰撞检测

成功！

我的球碰撞检测和响应工作得很好！

相关代码：

碰撞检测：

for (int i = 0; i < ballCount; i++)  
{  
    for (int j = i + 1; j < ballCount; j++)  
    {  
        if (balls[i].colliding(balls[j]))  
        {
            balls[i].resolveCollision(balls[j]);
        }
    }
}

这将检查每个球之间的碰撞但跳过冗余检查（如果您必须检查球 1 是否与球 2 碰撞，那么您不需要检查球 2 是否与球 1 碰撞。此外，它会跳过检查与自身的碰撞）。

然后，在我的球类中，我有我的 colliding() 和 resolveCollision() 方法：

public boolean colliding(Ball ball)
{
    float xd = position.getX() - ball.position.getX();
    float yd = position.getY() - ball.position.getY();

    float sumRadius = getRadius() + ball.getRadius();
    float sqrRadius = sumRadius * sumRadius;

    float distSqr = (xd * xd) + (yd * yd);

    if (distSqr <= sqrRadius)
    {
        return true;
    }

    return false;
}

public void resolveCollision(Ball ball)
{
    // get the mtd
    Vector2d delta = (position.subtract(ball.position));
    float d = delta.getLength();
    // minimum translation distance to push balls apart after intersecting
    Vector2d mtd = delta.multiply(((getRadius() + ball.getRadius())-d)/d); 


    // resolve intersection --
    // inverse mass quantities
    float im1 = 1 / getMass(); 
    float im2 = 1 / ball.getMass();

    // push-pull them apart based off their mass
    position = position.add(mtd.multiply(im1 / (im1 + im2)));
    ball.position = ball.position.subtract(mtd.multiply(im2 / (im1 + im2)));

    // impact speed
    Vector2d v = (this.velocity.subtract(ball.velocity));
    float vn = v.dot(mtd.normalize());

    // sphere intersecting but moving away from each other already
    if (vn > 0.0f) return;

    // collision impulse
    float i = (-(1.0f + Constants.restitution) * vn) / (im1 + im2);
    Vector2d impulse = mtd.normalize().multiply(i);

    // change in momentum
    this.velocity = this.velocity.add(impulse.multiply(im1));
    ball.velocity = ball.velocity.subtract(impulse.multiply(im2));

}

源代码：球对球对撞机的完整源代码。

如果有人对如何改进这个基本的物理模拟器有一些建议，请告诉我！我还没有补充的一件事是角动量，所以球会更真实地滚动。还有其他建议吗？发表评论！

score 122 · Accepted Answer

要检测两个球是否碰撞，只需检查它们的中心之间的距离是否小于半径的两倍。要在球之间进行完美的弹性碰撞，您只需要担心碰撞方向上的速度分量。两个球的另一个组件（与碰撞相切）将保持不变。您可以通过创建一个指向从一个球到另一个球的方向的单位矢量来获得碰撞分量，然后将点积与球的速度矢量相乘。然后，您可以将这些分量代入一维完美弹性碰撞方程。

维基百科对整个过程有很好的总结。对于任何质量的球，新的速度可以使用以下公式计算（其中 v1 和 v2 是碰撞后的速度，u1、u2 是碰撞前的速度）：

$v_{1} = \frac{u_{1}(m_{1}-m_{2})+2m_{2}u_{2}}{m_{1}+m_{2}}$

$v_{2} = \frac{u_{2}(m_{2}-m_{1})+2m_{1}u_{1}}{m_{1}+m_{2}}$

如果球具有相同的质量，则只需切换速度。这是我写的一些代码，它做类似的事情：

void Simulation::collide(Storage::Iterator a, Storage::Iterator b)
{
    // Check whether there actually was a collision
    if (a == b)
        return;

    Vector collision = a.position() - b.position();
    double distance = collision.length();
    if (distance == 0.0) {              // hack to avoid div by zero
        collision = Vector(1.0, 0.0);
        distance = 1.0;
    }
    if (distance > 1.0)
        return;

    // Get the components of the velocity vectors which are parallel to the collision.
    // The perpendicular component remains the same for both fish
    collision = collision / distance;
    double aci = a.velocity().dot(collision);
    double bci = b.velocity().dot(collision);

    // Solve for the new velocities using the 1-dimensional elastic collision equations.
    // Turns out it's really simple when the masses are the same.
    double acf = bci;
    double bcf = aci;

    // Replace the collision velocity components with the new ones
    a.velocity() += (acf - aci) * collision;
    b.velocity() += (bcf - bci) * collision;
}

至于效率，Ryan Fox 是对的，你应该考虑将区域划分为多个部分，然后在每个部分中进行碰撞检测。请记住，球可能会在部分边界上与其他球发生碰撞，因此这可能会使您的代码更加复杂。不过，在你有几百个球之前，效率可能并不重要。对于奖励积分，您可以在不同的核心上运行每个部分，或者在每个部分内拆分处理碰撞。

score 50 · Accepted Answer

好吧，几年前我制作了像你在这里介绍的程序。
有一个隐藏的问题（或许多，取决于观点）：

如果球的速度太高，你可能会错过碰撞。

而且，几乎在 100% 的情况下，您的新速度都是错误的。好吧，不是速度，而是位置。您必须在正确的位置精确计算新速度。否则，您只需在一些小的“错误”量上移动球，这可从上一个离散步骤中获得。

解决方案很明显：你必须拆分时间步长，首先你移动到正确的位置，然后碰撞，然后在剩下的时间里移动。

score 20 · Accepted Answer

20

您应该使用空间分区来解决这个问题。

阅读二进制空间分区和四叉树

于 2008-12-06T03:43:14.467 回答

score 13 · Accepted Answer

作为对 Ryan Fox 建议将屏幕分割成区域的建议的澄清，并且只检查区域内的碰撞......

例如，将游戏区域分成一个方格（可以任意说每边有 1 个单位长度），并检查每个方格内的碰撞。

这绝对是正确的解决方案。它的唯一问题（正如另一位海报指出的那样）是跨界碰撞是一个问题。

解决方案是在与第一个网格相距 0.5 单位的垂直和水平偏移处覆盖第二个网格。

然后，在第一个网格中跨越边界（因此未被检测到）的任何碰撞都将在第二个网格中的网格正方形内。只要您跟踪您已经处理过的冲突（因为可能存在一些重叠），您就不必担心处理边缘情况。所有碰撞都将在其中一个网格上的网格正方形内。

score 10 · Accepted Answer

减少碰撞检查次数的一个好方法是将屏幕分成不同的部分。然后，您只需将每个球与同一部分中的球进行比较。

score 8 · Accepted Answer

我在这里看到要优化的一件事。

虽然我确实同意当距离是它们的半径之和时球击中，但永远不应该实际计算这个距离！相反，计算它的平方并以这种方式使用它。没有理由进行昂贵的平方根运算。

此外，一旦发现碰撞，您必须继续评估碰撞，直到不再有碰撞为止。问题是第一个问题可能会导致其他问题，在您获得准确的图片之前必须解决这些问题。考虑一下如果球在边缘撞到球会发生什么？第二个球击中边缘并立即反弹到第一个球中。如果你撞到角落里的一堆球，你可能会遇到很多必须解决的碰撞，然后才能迭代下一个循环。

至于 O(n^2)，你所能做的就是最小化拒绝那些错过的成本：

1) 一个不动的球不能击中任何东西。如果地板上有合理数量的球，这可以节省大量测试。（请注意，您仍然必须检查是否有东西击中了静止的球。）

2）可能值得做的事情：将屏幕划分为多个区域，但线条应该是模糊的——区域边缘的球被列为所有相关（可能是 4 个）区域。我会使用 4x4 网格，将区域存储为位。如果两个球区域的区域与返回零，则测试结束。

3）正如我所提到的，不要做平方根。

score 6 · Accepted Answer

我找到了一个很棒的页面，其中包含有关 2D 碰撞检测和响应的信息。

http://www.metanetsoftware.com/technique.html (web.archive.org)

他们试图从学术的角度解释它是如何完成的。他们从简单的对象到对象的碰撞检测开始，然后转向碰撞响应以及如何扩大它。

编辑：更新链接

score 3 · Accepted Answer

你有两种简单的方法来做到这一点。杰伊已经涵盖了从球中心检查的准确方法。

更简单的方法是使用矩形边界框，将框的大小设置为球大小的 80%，这样就可以很好地模拟碰撞。

向你的球类添加一个方法：

public Rectangle getBoundingRect()
{
   int ballHeight = (int)Ball.Height * 0.80f;
   int ballWidth = (int)Ball.Width * 0.80f;
   int x = Ball.X - ballWidth / 2;
   int y = Ball.Y - ballHeight / 2;

   return new Rectangle(x,y,ballHeight,ballWidth);
}

然后，在你的循环中：

// Checks every ball against every other ball. 
// For best results, split it into quadrants like Ryan suggested. 
// I didn't do that for simplicity here.
for (int i = 0; i < balls.count; i++)
{
    Rectangle r1 = balls[i].getBoundingRect();

    for (int k = 0; k < balls.count; k++)
    {

        if (balls[i] != balls[k])
        {
            Rectangle r2 = balls[k].getBoundingRect();

            if (r1.Intersects(r2))
            {
                 // balls[i] collided with balls[k]
            }
        }
    }
}

score 3 · Accepted Answer

我看到它在这里和那里暗示，但您也可以先进行更快的计算，例如比较边界框的重叠，然后在第一次测试通过时进行基于半径的重叠。

边界框的加法/差分数学比半径的所有三角要快得多，并且大多数情况下，边界框测试将排除碰撞的可能性。但是，如果您随后使用 trig 重新测试，您将获得您正在寻找的准确结果。

是的，这是两个测试，但总体上会更快。

score 3 · Accepted Answer

3

这KineticModel是在 Java中引用的方法的实现。

于 2011-07-22T19:05:00.207 回答

score 2 · Accepted Answer

我使用 HTML Canvas 元素在 JavaScript 中实现了这段代码，它以每秒 60 帧的速度产生了精彩的模拟。我以随机位置和速度的十几个球的集合开始模拟。我发现在更高的速度下，一个小球和一个大得多的球之间的碰撞会导致小球看起来粘在大球的边缘，并在分离之前围绕大球移动了大约 90 度。（我想知道是否有其他人观察到这种行为。）

一些计算记录表明，在这些情况下，最小平移距离不足以防止相同的球在下一个时间步发生碰撞。我做了一些实验，发现我可以通过根据相对速度扩大 MTD 来解决这个问题：

dot_velocity = ball_1.velocity.dot(ball_2.velocity);
mtd_factor = 1. + 0.5 * Math.abs(dot_velocity * Math.sin(collision_angle));
mtd.multplyScalar(mtd_factor);

我验证了在此修复之前和之后，每次碰撞的总动能都是守恒的。mtd_factor 中的 0.5 值大约是发现在碰撞后总是导致球分离的最小值。

尽管此修复在系统的确切物理特性中引入了少量错误，但权衡是现在可以在浏览器中模拟非常快的球，而不会减少时间步长。

score 2 · Accepted Answer

通过问题中给出的圆碰撞检测改进检测圆的解决方案：

float dx = circle1.x - circle2.x,
      dy = circle1.y - circle2.y,
       r = circle1.r + circle2.r;
return (dx * dx + dy * dy <= r * r);

它避免了不必要的“如果有两个返回”和使用比必要更多的变量。

score 1 · Accepted Answer

经过反复试验，我使用了本文档的 2D 碰撞方法：https ://www.vobarian.com/collisions/2dcollisions2.pdf （OP 链接到）

我在一个使用 p5js 的 JavaScript 程序中应用了它，它运行良好。我之前曾尝试使用三角方程，虽然它们确实适用于特定的碰撞，但无论发生的角度如何，我都找不到适用于每次碰撞的三角方程。

本文档中解释的方法不使用任何三角函数，它只是简单的矢量运算，我向任何尝试实现球对球碰撞的人推荐这个，根据我的经验，三角函数很难推广。我请我大学的一位物理学家教我怎么做，他告诉我不要打扰三角函数，并向我展示了一种类似于文档中链接的方法。

注意：我的质量都是相等的，但这可以使用文档中提供的方程式推广到不同的质量。

这是我用于计算碰撞后产生的速度向量的代码：

    //you just need a ball object with a speed and position vector.
    class TBall {
        constructor(x, y, vx, vy) {
            this.r = [x, y];
            this.v = [0, 0];
        }
    }

    //throw two balls into this function and it'll update their speed vectors
    //if they collide, you need to call this in your main loop for every pair of 
    //balls.
    function collision(ball1, ball2) {
        n = [ (ball1.r)[0] - (ball2.r)[0], (ball1.r)[1] - (ball2.r)[1] ];
        un = [n[0] /  vecNorm(n), n[1] / vecNorm(n) ] ;
        ut = [ -un[1], un[0] ];   
        v1n = dotProd(un, (ball1.v));
        v1t = dotProd(ut, (ball1.v) );
        v2n = dotProd(un, (ball2.v) );
        v2t = dotProd(ut, (ball2.v) );
        v1t_p = v1t; v2t_p = v2t;
        v1n_p = v2n; v2n_p = v1n;
        v1n_pvec = [v1n_p * un[0], v1n_p * un[1] ]; 
        v1t_pvec = [v1t_p * ut[0], v1t_p * ut[1] ]; 
        v2n_pvec = [v2n_p * un[0], v2n_p * un[1] ]; 
        v2t_pvec = [v2t_p * ut[0], v2t_p * ut[1] ];
        ball1.v = vecSum(v1n_pvec, v1t_pvec); ball2.v = vecSum(v2n_pvec, v2t_pvec);
    }

score 0 · Accepted Answer

如果您有大量球，我会考虑使用四叉树。为了确定反弹的方向，只需使用基于碰撞法线的简单能量守恒公式。弹性、重量和速度会让它更真实一些。

score 0 · Accepted Answer

这是一个支持质量的简单示例。

private void CollideBalls(Transform ball1, Transform ball2, ref Vector3 vel1, ref Vector3 vel2, float radius1, float radius2)
{
    var vec = ball1.position - ball2.position;
    float dis = vec.magnitude;
    if (dis < radius1 + radius2)
    {
        var n = vec.normalized;
        ReflectVelocity(ref vel1, ref vel2, ballMass1, ballMass2, n);

        var c = Vector3.Lerp(ball1.position, ball2.position, radius1 / (radius1 + radius2));
        ball1.position = c + (n * radius1);
        ball2.position = c - (n * radius2);
    }
}

public static void ReflectVelocity(ref Vector3 vel1, ref Vector3 vel2, float mass1, float mass2, Vector3 intersectionNormal)
{
    float velImpact1 = Vector3.Dot(vel1, intersectionNormal);
    float velImpact2 = Vector3.Dot(vel2, intersectionNormal);

    float totalMass = mass1 + mass2;
    float massTransfure1 = mass1 / totalMass;
    float massTransfure2 = mass2 / totalMass;

    vel1 += ((velImpact2 * massTransfure2) - (velImpact1 * massTransfure2)) * intersectionNormal;
    vel2 += ((velImpact1 * massTransfure1) - (velImpact2 * massTransfure1)) * intersectionNormal;
}

graphics - 球对球碰撞 - 检测和处理

成功！

15 回答 15

Related

Reference