algorithm - 距离矩阵的近似估计

Question

我有一组 N 个对象，我想计算一个 NxN 距离矩阵。有时我的 N 个对象集非常大，我想通过仅计算距离比较的子集来计算 NxN 距离矩阵的近似值。

谁能指出我计算全距离矩阵近似值的方向？我有一些想法，但我想避免重新发明轮子。

编辑：算法类型的一个示例将利用这样一个事实，即如果对象 A 和对象 B 之间的距离非常小，并且对象 B 和对象 C 之间的距离非常小，则必须有一些物体 A 和 C 之间的距离很短。

score 2 · Accepted Answer

我有同样的问题，最终为它编写了 Python 代码：

README.md 解释了如何使用三角不等式来更新每个距离的上限和下限。

只需将 Python 文件作为脚本在二维空间中运行即可。绘制的线是实际计算的唯一距离。

在我的版本中，节省的时间与拥有大量对象无关。正如我所写的，它是一个 O(n^4) 算法，所以如果对象的数量很大，它实际上比只计算所有距离更糟糕。但是当对象数量适中并且距离函数的计算成本非常高时，我的方法会节省时间。它假设执行多个 O(n^2) 操作而不是单个距离测量更快。

如果 n 很大，您可以寻找更便宜的方法来决定接下来要计算的距离（不涉及距离边界矩阵的 n^2 个条目的算术）。您也可能不需要每次执行此代码时都更新所有 2*n^2 边界。

score 1 · Accepted Answer

您的“对象”在网络上吗？如果对象在网络中，您可以使用this或this来生成所有对的最短路径。如果没有，我认为你几乎会被计算出的所有 nxn 距离所困扰。

score 1 · Accepted Answer

老实说，我认为这取决于您希望近似值有多接近以及您的子集有多大。如果您只想对矩阵的外观有一些整体感觉，您可以对随机子集（包括最大和最小节点）进行简单的线性插值，以获得非常准确的 (tm) 结果。

$线性插值$

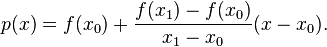
我认为这里真正的技巧是找出启发式（线性、二次等插值）和子集大小。您还可以计算出各种子集的距离矩阵，然后用某种方法（线性、球面线性、三次）对这些矩阵进行插值。

根据您的初始样本，这几乎是一个启发式的试验和错误，直到您“哦，这对我需要的足够好”。

score 1 · Accepted Answer

您需要的解决方案类似于我们通常在图中看到的，您可以使用All pair shortest path来求距离，您也可以查看johnson's algorithm

4 回答 4