11

我有一个 2D 形状存储为 SVG 中的路径元素。形状由贝塞尔曲线和线段组成。

我还有一组沿我使用弧长参数化生成的形状的等距点。

如何使用 SVG 或这些点来确定形状的中轴？

我正在使用 Python，但任何类型的伪代码或算法建议将不胜感激。

以下是我正在处理的形状类型的示例，红点是我沿曲线的采样点。

例子

4

2 回答 2

22

有点晚了，但这里有：

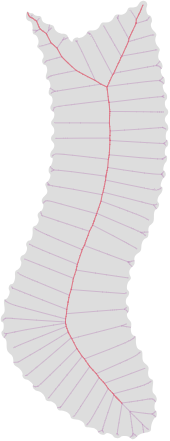
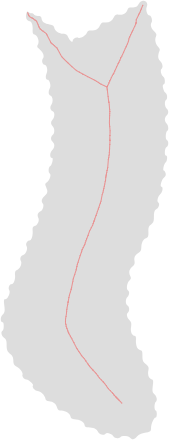
中间轴和比例轴变换 比例轴变换 中轴变换 2 爪 三爪

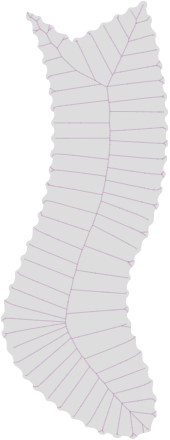
上面的图片显示：（我已经使用在线工具将 OP 的图像转换为 SVG，因此边界参差不齐，这是红点的伪影） 1. 叠加的中间轴和比例轴变换（MAT和SAT）。2. 仅缩放轴变换。3. 仅中轴变换。4. 许多2 爪之一（见下文）。5. SAT中的单三叉戟（ MAT中有很多）。

要找到中轴 (MA)或中轴变换 (MAT)（上图中的紫色曲线），可以使用以下算法（基于 Choi、Choi、Moon 和 Wee的论文- 请参阅此处的演示实现，它还处理相交的形状和带孔的形状）。其他算法也存在。

该算法比查找二进制图像（例如位图）骨架（又名草火或离散变换）更难实现，但具有几个优点（例如可分析）。为简化起见，下面的讨论仅处理没有孔的简单（非相交）形状的情况。

一些定义

  • 曲线- 参数t ∈ [0,1] 的参数贝塞尔曲线。换句话说，矢量图形中使用的典型曲线。
  • 形状（Ω） -（直接取自论文的定义）-“由有限数量的相互不相交的简单闭合曲线限制的 ℝ² 中连接的有界开放子集的闭合。” 出于此答案的目的，可以进一步假设该形状没有孔。简单来说，它是由许多曲线给出的边界所包围的区域- 上图中的填充灰色部分。
  • 边界-形状的边界。换句话说，曲线的索引序列使得任何曲线在t = 0 处的起点对应于前一条曲线在t = 1 处的终点。边界被假定为正向（即沿边界逆时针方向行走，形状将始终在您的左侧）。
  • 边界点- 形状边界上的任何点，完全由标识曲线的索引和t 曲线参数标识。
  • 最大圆盘- 形状内的圆盘没有被形状内的任何其他圆盘遮挡。每个最大圆盘可以由 1 个或多个（通常为 2 个）边界点s 及其中心点来识别。
  • n-prong -在 n 个点切向接触形状边界的最大圆盘。
  • 分支点- n >= 3 的n 叉 最大磁盘中心。换句话说，MA 上的一个点在MA平面树中形成一个顶点。
  • 中轴 (MA) - 所有n 叉的中心的联合。
  • 中轴变换 (MAT) - 所有n 叉的并集。换句话说，最大圆盘的半径包含在定义中。
  • 接触点 (cp) -连接到 已找到的唯一最大圆盘的边界点。
  • 尖角- 一个边界点，通常在曲线参数t = 0 或 t = 1 处，不可微分（不平滑）并且形成内角 < 180°。
  • 钝角- 与锐角相同，但角度 > 180°。
  • Cp 图- 顶点为接触点s的图（不一定是平面图）， 因此还包含有关所有找到 的最大磁盘s 以及整个MAT的信息。图中的每个顶点 ( cp ) 具有以下边：
    • next -通过绕边界逆时针行走从当前接触点找到的第一个接触点。
    • prev -绕边界顺时针从当前点找到的第一个接触点。
    • next-around - 以逆时针方向绕过 最大圆盘找到的第一个接触点。
    • prev-around -以顺时针方向绕过 最大圆盘找到的第一个接触点。我们可以将上述每一个视为一个接触点上的运算符 (.)，通过沿一条边返回另一个接触点，例如，如果a是一个接触点，那么a。接下来是另一个联络点。

一些笔记

  • 中轴变换在每个1 叉中心（包括尖角s）形成一棵无根平面树；如果形状有孔，则MAT是平面图。
  • 您可以通过对MAT应用Scale Axis Transform (SAT)（上图中的红色曲线）来消除形状边界上的噪声 。该 演示基于这项 研究实现了这样的转换。但是，该演示通过确保SAT是MAT的子集并保证拓扑保留来改进算法。

算法概述

  1. 找到所有1-prongs ; 它们正是中轴树叶。这些是尖角和接触具有最大局部向内曲率的边界点的1 叉。将1 叉的接触点s添加到cp-graph 中。请注意，由于1-prong仅具有一个接触点，因此next-around 和prev-around的边缘将再次返回找到的接触点。
  2. 对于一组有代表性的边界点s（例如OP给出的那些红点），计算它们的最大圆盘s。它们通常是2 叉的。（参见下文“寻找 2 管脚”）。通过连接适当的边将它们的接触点s 添加到cp 图。请注意，在这种情况下，由于我们找到了2-prongs，因此如果next-around （或prev-around）被跟踪两次，则将返回相同的接触点。

  3. 最后找到 n >= 3 的n 叉。从每个接触点开始：

    1. 通过从接触点（例如cp1）开始并应用cp1来遍历cp-graph。接下来。next-around重复直到你回到 cp1。

    2. 如果发生上述 1 或 2 次迭代，则移动到边界 上的下一个接触点（使用next）。但是，如果需要 3 次或更多次迭代，则可以证明存在3 叉分支点，并且应该在cp1和cp1之间的每个边界块 上插入接触点s 。接下来。

      在这种情况下，插入3-prong（请参阅下文了解如何找到这些）并返回第 1 步，再次从cp1开始。

    3. 重复步骤 1 和 2，直到找到所有3 爪。
  4. 现在已经隐含地找到了MAT的结构。要提取MAT，需要遍历cp-graph。选择任何 接触点（称为cp1）作为根（为简单起见，我们假设它链接到2-prong），然后应用下一个（称为cp2）。现在可以从cp1的链接最大圆盘 中心画一条线到cp2的最大圆盘中心。这条线是MA子集的近似值。由于我们知道接触点处的边界切线，因此通过点之间的插值可以获得更好的近似值. 让两条线的端点成为二次贝塞尔曲线的端点。由于MA在两个最大圆盘中心的方向是准确已知的（通过 2 个边界切线的平均值），我们在端点处也有二次贝塞尔曲线的导数，我们可以在两点之间构建最佳近似二次贝塞尔曲线. 如果cp2链接到一个3 叉，则意味着由MA分叉（即分支 ot 叉）形成的平面树，我们需要遵循MA的两条 边（例如，通过使用堆栈或递归）。另一方面，如果 cp2链接到MA的1 叉叶已经到达并且该边的遍历停止。事实上，由于MA形成一个平面树，因此遍历算法与任何其他树数据结构的遍历算法基本相同。

找到一个 2 叉

  1. 我将在这里总结，但 Choi 等人的论文。这部分解释得很清楚，很容易理解。

    在边界上选择一个点，它将成为我们2 叉的第一个接触点，并将其命名为bp1。从边界点画一条向内的法线 （即要找到的2 叉的第一个“叉”）。现在迭代：

    1. 选择一个点p1（沿这条射线与 bp1 的距离为 d1 ），其d1足够大，使得一个圆（在bp1处切线绘制，中心在射线上）将在至少一个点上 切割边界。
    2. 找到最接近p1的边界点，称为bp2。最后，找到与bp1和bp2等距的射线上的点并将其命名为p2。
    3. 使用新的p2返回第 2 步p1。
    4. 重复步骤 2 和 3，直到p1到两个 边界点s 的距离在某个公差范围内相等。现在已经发现2 叉， bp1和bp2 是它的两个接触点s， p1是它的中心。

寻找一个三叉戟

在这里，我们通过构造外接圆而不是使用势函数来偏离论文。

  1. 选择边界点( cp1 ) 链接的最大圆盘中心作为要找到的3 叉中心的初始猜测 。称之为p。
  2. 分别找到与3+边界块s中的每一个最接近的 3 个点。
  3. 构造这些点的外接圆并将其中心用作新点p。
  4. 重复步骤 2 和 3，直到从p到 3 个边界块的距离 等于某个公差范围内。
  5. 将找到的 3 个边界点标记为 3爪的接触点。点p是3-prong的中心。

请随时询问是否有任何不清楚的地方。

于 2018-10-13T19:55:33.710 回答
1

你可以从 skimage (scikit-image) 看到代码。您将找到骨架化代码和中间轴代码 (skimage.morphology.medial_axis)

源代码可在此地址获得：https ://github.com/scikit-image/scikit-image/blob/v0.12.2/skimage/morphology/_skeletonize.py#L103

该算法将图像的中轴变换计算为其距离变换的脊。

算法的不同步骤如下

A lookup table is used, that assigns 0 or 1 to each configuration of
   the 3x3 binary square, whether the central pixel should be removed
   or kept. 

We want a point to be removed if it has more than one neighbor
   and if removing it does not change the number of connected components.


The distance transform to the background is computed, as well as
   the cornerness of the pixel.

The foreground (value of 1) points are ordered by
   the distance transform, then the cornerness.

A cython function is called to reduce the image to its skeleton. It
   processes pixels in the order determined at the previous step, and
   removes or maintains a pixel according to the lookup table. 

Because
   of the ordering, it is possible to process all pixels in only one
   pass.

我希望它会帮助你

于 2017-02-07T13:14:34.490 回答