2

对于任何三个给定的集合 A、B 和 C：有没有办法（以编程方式）确定 A 的元素是否是 B 和 C 的合取（编辑：交集）的一部分？

例如：
A：所有大于 3 的数字
B：所有小于 7 的
数字 C：所有等于 5 的数字

在这种情况下，集合 A 中有一个元素，即数字 5，它适合。我将其作为规范来实现，所以这个数值范围只是一个例子。A、B、C 可以是任何东西。

4

3 回答 3

5

编辑： 谢谢尼基！

如果B.Count <= C.Count <= A.Count.

D = GetCommonElements(B,C);
if( D.Count>0 && GetCommonElements(D,A).Count >0)
{
    // what you want IS NOT EMPTY
}
else
{
    // what you want IS EMPTY
}

SET GetCommonElements(X,Y)
{
    common = {}
    for x in X:
       if Y.Contains(x):
         common.Add(x);
    return common;
}

查看有效集合交集算法。

我们可以使用集合的分配律

替代文字

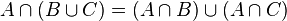
if(HasCommonElements(A,B) || HasCommonElements(A,C))
{
    // what you want IS NOT EMPTY
}
else
{
    // what you want IS EMPTY
}


bool HasCommonElements(X,Y)
{
    // if at least one common element is found return true(immediately)

    return false
}
于 2010-04-13T19:47:06.233 回答
1

如果我正确理解您的问题，您想以编程方式计算 3 组的交集，对吗？你想看看A中是否有一个元素存在于B和C的交集，或者换句话说，你想知道A、B和C的交集是否非空。

许多语言已经设置了容器和交叉算法，所以你应该能够使用它们。您在 OCaml 中的示例：

module Int = struct
    type t = int
    let compare i j = if i<j then -1 else if i=j then 0 else 1
end;;

module IntSet = Set.Make(Int);;

let a = List.fold_left (fun a b -> IntSet.add b a) IntSet.empty [4;5;6;7;8;9;10];;
let b = List.fold_left (fun a b -> IntSet.add b a) IntSet.empty [0;1;2;3;4;5;6];;
let c = IntSet.add 5 IntSet.empty;;

let aIbIc = IntSet.inter (IntSet.inter b c) a;;
IntSet.is_empty aIbIc;;

这输出假，因为 ab 和 c 的交集是非空的（包含 5）。这当然依赖于集合的元素是可比较的事实（在示例中，函数 compare 在 Int 模块中定义了此属性）。

或者在 C++ 中：

#include<iostream>
#include<set>
#include<algorithm>
#include<iterator>

int main()
{
    std::set<int> A, B, C;

    for(int i=10; i>3; --i)
        A.insert(i);
    for(int i=0; i<7; ++i)
        B.insert(i);
    C.insert(5);

    std::set<int> ABC, BC;
    std::set_intersection(B.begin(), B.end(), C.begin(), C.end(), std::inserter(BC, BC.begin()));
    std::set_intersection(BC.begin(), BC.end(), A.begin(), A.end(), std::inserter(ABC, ABC.begin()));

    for(std::set<int>::iterator i = ABC.begin(); i!=ABC.end(); ++i)
    {
        std::cout << *i << " ";
    }
    std::cout << std::endl;

    return 0;
}
于 2010-04-13T23:13:31.620 回答
0

The question needs further clarification. First, do you want to work with symbolic sets given by a range? And secondly, is it a one time question or is it going to be repeated in some form (if yes, what are the stable parts of the question?)?

If you want to work with ranges, then you could represent these with binary trees and define union and intersection operations on these structures. Building the tree would require O(n log n) and finding the result would require O(log n). This would not pay off with only tree sets, but it would be flexible to efficiently support any combination of ranges (if that is what you thought by 'it can be anything').

另一方面，如果有任何含义，任何元素集，那么唯一的选择就是枚举元素。在这种情况下，在集合 B 和 C 上构建 B+ 树也需要 O(n log n) 时间，但这里 n 是元素的数量，在第一种情况下，n 是范围的数量。后者可能要大几个数量级，当然它只能代表有限数量的元素。

于 2010-04-14T17:59:24.743 回答