3

设想

我正在尝试对 Java GUI 应用程序中的数据集实施监督学习。用户将获得要检查的项目或“报告”列表，并将根据一组可用标签对其进行标记。一旦监督学习完成，标记的实例将被提供给学习算法。这将尝试根据用户想要查看它们的可能性对其余项目进行排序。

为了充分利用用户的时间，我想预先选择将提供有关整个报告集合的最多信息的报告，并让用户标记它们。据我了解，要计算这一点，有必要找到每个报告的所有互信息值的总和，并按该值对它们进行排序。然后，来自监督学习的标记报告将用于形成贝叶斯网络，以找到每个剩余报告的二进制值的概率。

例子

在这里，一个人为的例子可能有助于解释，并且当我无疑使用了错误的术语时可能会消除混乱:-) 考虑一个应用程序向用户显示新闻故事的例子。它根据显示的用户偏好选择首先显示哪些新闻报道。具有相关性的新闻故事的特征country of origin是category或date。因此，如果用户将来自苏格兰的单个新闻故事标记为有趣，它会告诉机器学习器，来自苏格兰的其他新闻故事对用户感兴趣的机会增加。类似于 Sport 等类别或 2004 年 12 月 12 日等日期。

可以通过为所有新闻故事选择任何顺序（例如，按类别、按日期）或随机排序它们，然后在用户进行时计算偏好来计算这种偏好。我想做的是让用户查看少量特定新闻故事并说出他们是否对它们感兴趣（监督学习部分），从而在该排序上获得一种“领先优势”。要选择向用户展示哪些故事，我必须考虑整个故事集合。这就是互信息的用武之地。对于每个故事，我想知道当它被用户分类时，它可以告诉我多少关于所有其他故事的信息。例如，如果有大量来自苏格兰的故事，我想让用户（至少）对其中一个进行分类。其他相关特征（例如类别或日期）也类似。目标是找到在分类时提供关于其他报告的最多信息的报告示例。

问题

因为我的数学有点生疏，而且我是机器学习的新手，所以在将互信息的定义转换为 Java 实现时遇到了一些麻烦。维基百科将互信息的方程式描述为：

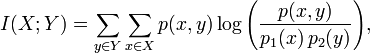
互信息方程

但是，我不确定这是否真的可以在没有分类的情况下使用，并且学习算法还没有计算任何东西。

在我的示例中，假设我有大量新的、未标记的此类实例： 

public class NewsStory {
    private String countryOfOrigin;
    private String category;
    private Date date;
    // constructor, etc.
}

在我的具体场景中，字段/特征之间的相关性是基于精确匹配的，因此，例如，一天和 10 年的日期差异在它们的不等式上是等效的。

The factors for correlation (e.g. is date more correlating than category?) are not necessarily equal, but they can be predefined and constant. Does this mean that the result of the function p(x,y) is the predefined value, or am I mixing up terms?

The Question (finally)

How can I go about implementing the mutual information calculation given this (fake) example of news stories? Libraries, javadoc, code examples etc. are all welcome information. Also, if this approach is fundamentally flawed, explaining why that is the case would be just as valuable an answer.

PS. I am aware of libraries such as Weka and Apache Mahout, so just mentioning them is not really useful for me. I'm still searching through documentation and examples for both these libraries looking for stuff on Mutual Information specifically. What would really help me is pointing to resources (code examples, javadoc) where these libraries help with mutual information.

4

2 回答 2

4

I am guessing that your problem is something like...

"Given a list of unlabeled examples, sort the list by how much the predictive accuracy of the model would improve if the user labelled the example and added it to the training set."

If this is the case, I don't think mutual information is the right thing to use because you can't calculate MI between two instances. The definition of MI is in terms of random variables and an individual instance isn't a random variable, it's just a value.

The features and the class label can be though of as random variables. That is, they have a distribution of values over the whole data set. You can calculate the mutual information between two features, to see how 'redundant' one feature is given the other one, or between a feature and the class label, to get an idea of how much that feature might help prediction. This is how people usually use mutual information in a supervised learning problem.

I think ferdystschenko's suggestion that you look at active learning methods is a good one.

In response to Grundlefleck's comment, I'll go a bit deeper into terminology by using his idea of a Java object analogy...

Collectively, we have used the term 'instance', 'thing', 'report' and 'example' to refer to the object being clasified. Let's think of these things as instances of a Java class (I've left out the boilerplate constructor):


class Example
{ String f1;
  String f2;
}

Example e1 = new Example("foo", "bar");
Example e2 = new Example("foo", "baz");

The usual terminology in machine learning is that e1 is an example, that all examples have two features f1 and f2 and that for e1, f1 takes the value 'foo' and f2 takes the value 'bar'. A collection of examples is called a data set.

取数据集中所有样本的f1的所有值，这是一个字符串列表，也可以认为是一个分布。我们可以将特征视为一个随机变量，列表中的每个值都是从该随机变量中提取的样本。例如，我们可以计算 f1 和 f2 之间的 MI。伪代码将类似于： 

mi = 0
for each value x taken by f1:
{  sum = 0
   for each value y taken by f2:
   {  p_xy = number of examples where f1=x and f2=y
      p_x = number of examples where f1=x
      p_y = number of examples where f2=y
      sum += p_xy * log(p_xy/(p_x*p_y))
   }
   mi += sum
}

但是，您无法计算 e1 和 e2 之间的 MI，只是没有这样定义。

于 2010-01-08T00:20:24.387 回答
1

I know information gain only in connection with decision trees (DTs), where in the construction of a DT, the split to make on each node is the one which maximizes information gain. DTs are implemented in Weka, so you could probably use that directly, although I don't know if Weka lets you calculate information gain for any particular split underneath a DT node.

Apart from that, if I understand you correctly, I think what you're trying to do is generally referred to as active learning. There, you first need some initial labeled training data which is fed to your machine learning algorithm. Then you have your classifier label a set of unlabeled instances and return confidence values for each of them. Instances with the lowest confidence values are usually the ones which are most informative, so you show these to a human annotator and have him/her label these manually, add them to your training set, retrain your classifier, and do the whole thing over and over again until your classifier has a high enough accuracy or until some other stopping criterion is met. So if this works for you, you could in principle use any ML-algorithm implemented in Weka or any other ML-framework as long as the algorithm you choose is able to return confidence values (in case of Bayesian approaches this would be just probabilities).

With your edited question I think I'm coming to understand what your aiming at. If what you want is calculating MI, then StompChicken's answer and pseudo code couldn't be much clearer in my view. I also think that MI is not what you want and that you're trying to re-invent the wheel.

Let's recapitulate: you would like to train a classifier which can be updated by the user. This is a classic case for active learning. But for that, you need an initial classifier (you could basically just give the user random data to label but I take it this is not an option) and in order to train your initial classifier, you need at least some small amount of labeled training data for supervised learning. However, all you have are unlabeled data. What can you do with these?

Well, you could cluster them into groups of related instances, using one of the standard clustering algorithms provided by Weka or some specific clustering tool like Cluto. If you now take the x most central instances of each cluster (x depending on the number of clusters and the patience of the user), and have the user label it as interesting or not interesting, you can adopt this label for the other instances of that cluster as well (or at least for the central ones). Voila, now you have training data which you can use to train your initial classifier and kick off the active learning process by updating the classifier each time the user marks a new instance as interesting or not. I think what you're trying to achieve by calculating MI is essentially similar but may be just the wrong carriage for your charge.

Not knowing the details of your scenario, I should think that you may not even need any labeled data at all, except if you're interested in the labels themselves. Just cluster your data once, let the user pick an item interesting to him/her from the central members of all clusters and suggest other items from the selected clusters as perhaps being interesting as well. Also suggest some random instances from other clusters here and there, so that if the user selects one of these, you may assume that the corresponding cluster might generally be interesting, too. If there is a contradiction and a user likes some members of a cluster but not some others of the same one, then you try to re-cluster the data into finer-grained groups which discriminate the good from the bad ones. The re-training step could even be avoided by using hierarchical clustering from the start and traveling down the cluster hierarchy at every contradiction user input causes.

于 2010-01-05T09:54:54.327 回答