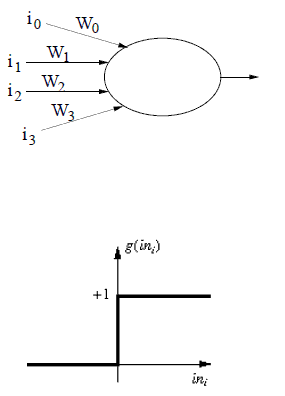
我正在尝试确定下面显示的人工神经元的输入 i1、i2 和 i3 的值（0 或 1），它将为其触发（i0 是偏置权重的输入，并且始终为 -1）。
权重是
W0 = 1.5
W1 = -1
W2 = 1，W3 = 2。
假设激活函数如下图所示。
请澄清你的答案，因为我做了几个例子，但我仍然无法完全理解这个理论:(
非常感谢，
玛丽·J。
PS。下图：
问问题
265 次
4 回答
3
似乎这只是求和in * Wn并确定 i1,2,3 的哪些组合产生积极结果的问题。只有 8 个排列，所以只需手动运行它。
于 2009-12-09T23:38:35.773 回答
3
对于神经元输出，您基本上有以下等式，其中i1、i2和i3可以分别具有值 0 或 1：
2*i3 + i2 - i1 - 1.5 >= 0
首先，让我们看一下最高的正加权值。如果i3为 0，则左侧最多可以得到 -0.5，因此i3必须为 1 才能获得非零输出。那么等式就变成了：
i2 - i1 + 0.5 >= 0
现在看看负加权值。如果i1为 0，则无论是什么，输出都将始终大于零i2。如果i1为 1，i2则必须为 1 才能有非零输出。
因此，您有这些组合可以创建非零输出：
i1 i2 i3
0 0 1
0 1 1
1 1 1
于 2009-12-09T23:53:34.827 回答
3
用更一般的方式解决这个问题，首先看什么是变量，什么是固定参数。
基本上，您得到了输入权重向量w= [1.5, -1, 1, 2]和传递函数 g(x) = (sign(x)+1)/2，并且您希望找到输入向量： w in '（作为行向量和列向量的乘积），因此：g(*) = +1
g( sum_over_i( w_i*in_i ) ) = 1 # product of vectors
g( w0*in0 + w1*in1 + w2*in2 + w3*in3 ) = 1 # roll out the sum
g( -1.5 - in1 + in2 + 2*in3 ) = 1 # replace the values of w and in
0.5*(sign(-1.5 - in1 + in2 + 2*in3)+1) = 1 # definition of g(x)
sign(-1.5 - in1 + in2 + 2*in3) = 1 # simplify
-1.5 - in1 + in2 + 2*in3 >= 0 # by def: [sign(x)=1 iff x>=0]
通常你会通过计算导数来求解这个方程，但由于输入只能取值0or 1，我们可以简单地枚举所有情况（有2^n或8情况）：
in1 in2 in3 -1.5-in1+in2+2*in3
-----------------------------------
0 0 0 -1.5
0 0 1 0.5 *
0 1 0 -0.5
0 1 1 1.5 *
1 0 0 -2.5
1 0 1 -0.5
1 1 0 -1.5
1 1 1 0.5 *
因此，我们得到上面表达式为正的in的值。
于 2009-12-10T00:50:54.493 回答
2
我对人工智能有粗略的了解，但据我所知：
输入总和 (Sigma i_n*W_n) 必须大于触发阈值。第二张图片告诉您触发阈值，第一张图片告诉您输入及其权重。
您只需要弄清楚哪些总和（不要忘记偏差）将导致所需的阈值/强度
于 2009-12-09T23:45:35.653 回答