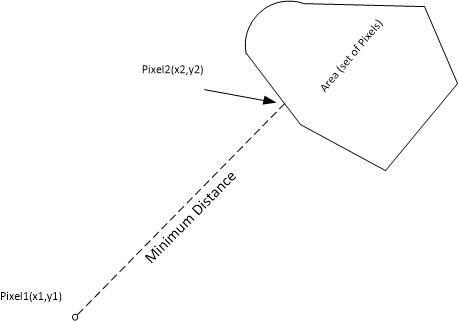
我试图在一个封闭区域中找到一个点(P2),它与点(P1)的距离最小。该区域由同质像素构成,形状不完美,也不一定是凸的。这基本上是从最短路径到达某个区域的问题。
整个空间以位图的形式存储在内存中。找到 P2 的最佳方法是什么?我应该使用随机搜索(优化)方法吗?优化方法没有给出确切的最小值,但它们比强制该区域的每个像素更快。我需要在几秒钟内执行数千个这样的决定。
该区域的 MinX,MinY,MaxX,MaxY 可用。
谢谢。
我试图在一个封闭区域中找到一个点(P2),它与点(P1)的距离最小。该区域由同质像素构成,形状不完美,也不一定是凸的。这基本上是从最短路径到达某个区域的问题。
整个空间以位图的形式存储在内存中。找到 P2 的最佳方法是什么?我应该使用随机搜索(优化)方法吗?优化方法没有给出确切的最小值,但它们比强制该区域的每个像素更快。我需要在几秒钟内执行数千个这样的决定。
该区域的 MinX,MinY,MaxX,MaxY 可用。

谢谢。
这是我的代码,它是使用离散坐标的离散版本:
提示:我用来求区域周长的方法很简单,就像你如何从陆地上知道海滩?答案:海滩从一侧被海覆盖,所以在我的图形矩阵中,NULL 参考是海,点是土地!
上课点:
class Point
{
public int x;
public int y;
public Point (int X, int Y)
{
this.x = X;
this.y = Y;
}
}
课区:
class Area
{
public ArrayList<Point> points;
public Area ()
{
p = new ArrayList<Point>();
}
}
离散距离实用程序类:
class DiscreteDistance
{
public static int distance (Point a, Point b)
{
return Math.sqrt(Math.pow(b.x - a.x,2), Math.pow(b.y - a.y,2))
}
public static int distance (Point a, Area area)
{
ArrayList<Point> cir = circumference(area);
int d = null;
for (Point b : cir)
{
if (d == null || distance(a,b) < d)
{
d = distance(a,b);
}
}
return d;
}
ArrayList<Point> circumference (Area area)
{
int minX = 0;
int minY = 0;
int maxX = 0;
int maxY = 0;
for (Point p : area.points)
{
if (p.x < minX) minX = p.x;
if (p.x > maxX) maxX = p.x;
if (p.y < minY) minY = p.y;
if (p.y > maxY) maxY = p.y;
}
int w = maxX - minX +1;
int h = maxY - minY +1;
Point[][] graph = new Point[w][h];
for (Point p : area.points)
{
graph[p.x - minX][p.y - minY] = p;
}
ArrayList<Point> cir = new ArrayList<Point>();
for (int i=0; i<w; i++)
{
for (int j=0; j<h; j++)
{
if ((i > 0 && graph[i-1][j] == null)
|| (i < (w-1) && graph[i+1][j] == null)
|| (j > 0 && graph[i][j-1] == null)
|| (i < (h-1) && graph[i][j+1] == null))
{
cir.add(graph[i][j]);
}
}
}
return cir;
}
}
我们必须假设您知道或可以轻松地在该区域内找到至少一个像素地址 (x0,y0)。最快的解决方案肯定是从该像素沿直线搜索,例如在加 x 方向上。或者,由于您有一个边界框,请选择指向最近边界的指南针点并朝该方向移动。
当你找到区域的边缘时,首先沿着边界搜索深度。 对于具有自相交和/或孔的一般多边形,这必须是一个完整且精心实施的 DFS,维护一组已访问的顶点。 只有当多边形很简单时,只记住最后访问的像素就足够了,以避免重复搜索已经搜索过的像素。
在 DFS 期间,计算每个边界像素的距离平方 p1 并跟踪最小值。
请注意,如果您真的迫切需要性能,这个距离平方可以增量更新,以用加法代替乘法。即,如果您知道d2=(x2-x1)^2+(y2-y1)^2然后递增x21 以围绕边界进行下一步,则新的平方距离为
((x2+1) - x1)^2 + (y2-y1)^2 = d2 + 2(x2 - x1) + 1
所以你可以d2用d2 += 2(x2 - x1) + 1. 乘以 2 当然只是左移,所以这很便宜。每个方向的步骤都有类似的非常便宜的更新。
一种方法可能是通过首先计算该区域的三角剖分来设置近似解;之后,只需检查三角形的角。这种方法可能是有益的,特别是如果在您计划的许多评估中,外点发生变化但形状本身没有变化。
您可以找到该区域矩形的中心,并使用两点之间的三角形来找到角度,然后使用函数 f(x) = mx + b 进行像素遍历,直到找到面积计算距离,然后旋转角度,直到找到最短路径。