5

我正在阅读有关Red-Black Trees 的wiki 。

有人可以详细说明第五个限制：

  1. 一个节点要么是红色的，要么是黑色的。

  2. 根是黑色的。

  3. 所有叶子 (NIL) 都是黑色的。（所有叶子的颜色都与根相同。）

  4. 每个红色节点的两个孩子都是黑色的。

  5. 从给定节点到其任何后代叶子的每条简单路径都包含相同数量的黑色节点。

我很难理解它，因为在插入的最后一个案例（wiki 上的案例 5）之后给出示例 RBT 的状态给我们：

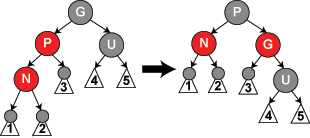
Wiki 红黑树

4 和 5 的黑色节点不是比 1,2 和 3 多一个吗？

4

4 回答 4

5

1、2、3、4、5都是子树。我们知道树 1、2 和 3 中根节点的颜色为黑色。我们不知道节点 1-5 中的任何一个是否是叶节点，因为这种插入情况可能已经在某个作为新插入节点的祖父母的 N 上递归调用（来自插入情况 3）。

旋转前后，子树 1、2、3 都在一个黑色节点之下（G before，P after），子树 4 和 5 在两个黑色节点之下（G 和 U before，P 和 U after）。子树 1、2 和 3 分别比子树 4 和 5 多一个黑色节点。

于 2013-02-24T14:19:17.380 回答
1

刚仔细看了下，图好像有问题。

由于N是刚刚插入的节点，这意味着在最后一个节点之前insert有P子 [1,3] 或 [2,3] （并且插入分别为 2 或 1）。所以在这种情况下，在最后一次插入之前P，U必须是红色的（而 4,5 是黑色的）。

于 2013-02-24T12:57:36.793 回答
1

恭喜 James 破译了 Wiki 图！没有错，只是模棱两可。

该页面的“谈话”选项卡提到“三角形不是代表叶子而是代表子树。一些子树的顶部有黑色圆圈，表示它们的根必须是黑色的。”

显然，没有圆圈的三角形代表子树（包括叶子），其根节点的颜色和树的深度是未知的（并且可能不相关）。

因此，这些图表根本没有提供足够的信息来判断是否违反了“规则 5”。我们必须将其视为既定事实，事实并非如此。

于 2013-02-24T18:07:33.447 回答
0

NIL 节点配置是完全可选的。它们是黑色的唯一原因是因为您希望默认保存额外的红色节点。以后可以根据需要将它们变为红色。

分配的黑色节点增加了黑色高度，这也是一个可选的高度差。因为必须在某处记录 NIL 标志，所以可以将其分配为黑色节点。

只能节省 1bit 地址空间；通常系统非常接近其极限。

于 2021-10-24T00:53:15.463 回答