2

我要实现

BigInteger.ModPow(1/BigInteger, 2,5);

但1/BigInteger总是 return 0，这导致结果也是0如此。我试图为 c# 寻找一些BigDecimal类，但我什么也没找到。即使没有，有没有办法计算这个BigDecimal？

4

3 回答 3

12

1/a|a|>1 时为 0，因为BigIntegers使用整数除法，其中忽略除法的小数部分。我不确定您对此有何期待。

我假设您想要模数的模乘逆，而不是小数。这个逆存在当且仅当且是互质的，即。amamgcd(a, m) = 1

链接的维基百科页面列出了计算模乘逆的两种标准算法：

  • 扩展欧几里得算法，适用于任意模
    它很快，但具有输入依赖的运行时。

    我手头没有 C# 代码，但是从维基百科移植伪代码应该是直截了当的。

  • 使用欧拉定理：
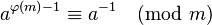
    $i^{-1} = i^{φ(n)-1}$
    这需要知道 φ(m)，即您需要知道 m 的质因数。m当是素数时，这是一个流行的选择，因此当它简单地变为 时 φ(m) = m-1 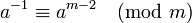$a^{-1} = a^{p-2}$。如果您需要恒定的运行时间并且您知道 φ(m)，那么这就是要走的路。

    在 C# 中，这变成BigInteger.ModPow(a, phiOfM-1, m)

于 2013-01-06T11:55:23.170 回答
1

/所选运算符的重载如下：

public static BigInteger operator /(
        BigInteger dividend,
        BigInteger divisor
)

请参阅BigInteger.Division 运算符。如您所见，如果结果介于0和之间1（很可能dividend是1您的情况），因为返回值是整数，所以返回。0

你想用这个ModPow方法做什么？您是否意识到这2,5是两个论点，二和五，而不是“二点五”？你的意图是“取平方模5”吗？

如果要浮点除法，可以使用：

1.0 / (double)yourBigInt

注意转换为double. yourBigInt如果太大，这可能会失去精度，甚至“下溢”为零。

于 2013-01-06T11:36:54.377 回答
0

例如，您需要在下一个中获取 d：
3*d = 1 (mod 9167368)

这同样是：
3*d = 1 + k * 9167368，其中 k = 1, 2, 3, ...

重写它：
d = (1 + k * 9167368)/3

您的 d 必须是具有最低k 的整数。
让我们写下公式：
d = (1 + k * fi)/e

public static int MultiplicativeInverse(int e, int fi)
        {
            double result;
            int k = 1;
            while (true)
            {
                result = (1 + (k * fi)) / (double) e;
                if ((Math.Round(result, 5) % 1) == 0) //integer
                {
                    return (int)result;
                }
                else
                {
                    k++;
                }
            }
        }

让我们测试一下这段代码：

Assert.AreEqual(Helper.MultiplicativeInverse(3, 9167368), 6111579); // passed
于 2015-03-08T21:26:30.057 回答