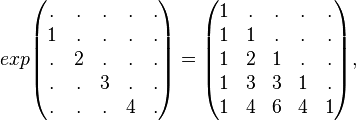c++ - 递归的帕斯卡三角

Question

注意： 我的班主任给了我这个问题作为作业......我没有被要求这样做，但请告诉我如何用递归来做

可以使用帕斯卡三角形计算二项式系数：

            1                   n = 0
         1     1
      1     2     1
   1     3     3     1
1     4     6     4     1       n = 4

三角形的每个新级别的两端都有 1；内部数字是它们上面的两个数字的总和。

任务：编写一个包含递归函数的程序，以使用帕斯卡三角技术生成幂 n 的二项式系数列表。例如，

输入 =2输出 = 1 2 1

输入 =4输出 =1 4 6 4 1

到目前为止完成了这个，但告诉我如何用递归来做到这一点......

#include<stdio.h>

int main()    
{
  int length,i,j,k;
//Accepting length from user
  printf("Enter the length of pascal's triangle : ");
  scanf("%d",&length);
//Printing the pascal's triangle
  for(i=1;i<=length;i++)
  {
      for(j=1;j<=length-i;j++)      
      printf(" ");
      for(k=1;k<i;k++)
          printf("%d",k);
      for(k=i;k>=1;k--)
          printf("%d",k);
      printf("\n");
  }
  return 0;    
}

Answer 1

方法一：

最简单的方法是使用二项式系数。使用此方法，您有 1 个递归方法：

// Here is your recursive function!
// Ok ok, that's cheating...
unsigned int fact(unsigned int n)
{
    if(n == 0) return 1;
    else return n * fact(n - 1);
}

unsigned int binom(unsigned int n, unsigned k)
{
    // Not very optimized (useless multiplications)
    // But that's not really a problem: the number will overflow
    // way earlier than you will notice any performance problem...
    return fact(n) / (fact(k) * fact(n - k));
}

std::vector<unsigned int> pascal(unsigned n)
{
    std::vector<unsigned int> res;
    for(unsigned int k = 0; k <= n; k++)
        res.push_back(binom(n,k));
    return res;
}

活生生的例子。

方法二：

此方法使用具有以下公式的构造：

在这里，唯一的函数是递归的，一次计算一行，将这些结果存储在一个数组中（为了缓存结果）。

std::vector<unsigned int> pascal(unsigned int n)
{
    // This variable is static, to cache results.
    // Not a problem, as long as mathematics do not change between two calls,
    // which is unlikely to happen, hopefully.
    static std::vector<std::vector<unsigned int> > triangle;

    if(triangle.size() <= n)
    {
        // Compute for i = last to n-1
        while(triangle.size() != n)
            pascal(triangle.size());

        // Compute for n
        if(n == 0)
            triangle.push_back(std::vector<unsigned int>(1,1));
        else
        {
            std::vector<unsigned int> result(n + 1, 0);
            for(unsigned int k = 0; k <= n; k++)
            {
                unsigned int l = (k > 0 ? triangle[n - 1][k - 1] : 0);
                unsigned int r = (k < n ? triangle[n - 1][k] : 0);
                result[k] = l + r;
            }
            triangle.push_back(result);
        }
    }

    // Finish
    return triangle[n];
}

活生生的例子。

其他方法：

还有一些其他奇特的方法，使用三角形的属性。你也可以使用矩阵的方式来生成它：

没有代码，因为它需要大量的基本代码（矩阵、矩阵的指数等），而且它并不是真正的递归。

另一方面，我认为这个问题绝对不是教授递归的正确问题。有很多更好的案例。