32

我需要一些建议。我正在开发一款类似于 Flow Free 的游戏，其中游戏板由网格和彩色点组成，用户必须将相同颜色的点连接在一起，而不会重叠其他线，并用完棋盘中的所有空闲空间。

我的问题是关于关卡创建的。我希望使关卡随机生成（并且至少应该能够自行解决，以便它可以给玩家提示）并且我对使用什么算法感到困惑。有什么建议么？

游戏目标

注意：图片显示了 Flow Free 的目标，这与我正在开发的目标相同。

谢谢你的帮助。:)

4

5 回答 5

29

考虑使用一对更简单、更易于管理的算法来解决您的问题：一种算法可以可靠地创建简单的、预先解决的板，另一种算法可以重新排列流程以使简单板更复杂。

如果您在x网格上使用n流，则第一部分构建一个简单的预求解板是微不足道的（如果您愿意的话） ：nn

  • 对于每个流...
    • 将头部点放在第一个开放列的顶部。
    • 将尾点放在该列的底部。

或者，您可以提供自己的手工入门板以传递到第二部分。这个阶段的唯一目标是构建一个有效的电路板，即使它只是微不足道的或预先确定的，所以保持简单是值得的。

第二部分，重新​​排列流，涉及循环每个流，查看哪个流可以与其相邻的流一起工作以增长和缩小：

  • 对于一些迭代...
    • 选择随机流f。
    • 如果f是最小长度（比如 3 个方格长），则跳到下一次迭代，因为我们现在不能收缩f。
    • 如果 的头部点f在另一个流中的点旁边g（如果有多个g可供选择，则随机选择一个）...
      • 将f的头部点沿其流程移动一格（即，将其向尾部移动一格）。f现在短了一个方格，还有一个空方格。（这个谜题现在没有解决。）
      • 将相邻的点从g移到由 腾出的空方格中f。现在有一个空的正方形g' 点从哪里移动。
      • 用来自 的流量填充那个空白点g。现在g比本次迭代开始时长一平方。（谜题也重新得到解决。）
    • f对' 的尾点重复上一步。

目前的方法是有限的（点总是邻居），但很容易扩展：

  • 添加一个步骤来遍历 flow 的主体f，寻找更巧妙的方法来与其他流交换空间......
  • 添加一个防止点移动到旧位置的步骤...
  • 添加您提出的任何其他想法。

这里的整体解决方案可能不如您所追求的理想解决方案，但现在您有两个简单的算法，您可以进一步充实它们，以充当一个大型、包罗万象的算法。最后，我认为这种方法是易于管理的，不神秘，而且易于调整，如果不出意外，这是一个很好的起点。

更新：我根据上述步骤编写了一个概念验证。从下面的第一个 5x5 网格开始，该过程产生了随后的 5 个不同的板。有些很有趣，有些则不是，但它们对于一种已知的解决方案总是有效的。

初始点
图 1 - 起始帧

5 个随机结果（抱歉截图不对齐）
图 2 图 3 图 4 图 5 图 6

和一个随机的 8x8 的好测量。起点是与上面相同的简单列方法。

图 7

于 2012-10-17T04:03:21.133 回答
9

创建这样一个关卡最直接的方法是找到解决它的方法。这样，您基本上可以生成任何随机启动配置，并通过尝试解决它来确定它是否是有效关卡。这将产生最多样化的关卡。

即使您找到了一种以其他方式生成关卡的方法，您仍然需要应用此求解算法来证明生成的关卡是好的；）

蛮力枚举

如果电路板有 NxN 单元大小，并且还有 N 种颜色可用，那么暴力枚举所有可能的配置（无论它们是否形成起始节点和结束节点之间的实际路径）将需要：

  • 总共 N^2 个单元格
  • 2N 个单元已被起始节点和结束节点占用
  • N^2 - 2N 个颜色尚未确定的单元格
  • N种颜色可供选择。
  • N^(N^2 - 2N) 种可能的组合。

所以，

  • 对于 N=5，这意味着 5^15 = 30517578125 个组合。
  • 对于 N=6，这意味着 6^24 = 4738381338321616896 组合。

换句话说，可能的组合数量一开始就相当多，但一旦你开始让棋盘变大，它的增长速度也会快得离谱。

限制每种颜色的单元格数量

显然，我们应该尽量减少配置的数量。这样做的一种方法是考虑每种颜色的开始和结束单元格之间的最小距离（“dMin”） - 我们知道至少应该有这么多具有​​该颜色的单元格。可以使用简单的洪水填充或 Dijkstra 算法来计算最小距离。（注意，整个下一节只讨论单元的数量，但没有说明它们的位置）

在您的示例中，这意味着（不计算开始和结束单元格）

dMin(orange) = 1
dMin(red) = 1
dMin(green) = 5
dMin(yellow) = 3
dMin(blue) = 5

这意味着，在尚未确定颜色的 15 个单元中，必须至少有 1 个橙色、1 个红色、5 个绿色、3 个黄色和 5 个蓝色单元，也就是总共 15 个单元。对于这个特定的例子，这意味着通过最短路径（其中一个）连接每个颜色的开始和结束单元格会填满整个电路板 - 即，在用最短路径填充电路板后，不会留下未着色的单元格。（这应该被认为是“运气”，并非每个板的启动配置都会导致这种情况发生）。

通常，在这一步之后，我们有许多可以自由着色的单元格，我们称这个数字为 U。对于 N=5，

U = 15 - (dMin(orange) + dMin(red) + dMin(green) + dMin(yellow) + dMin(blue))

因为这些单元格可以采用任何颜色，所以我们还可以确定可以具有特定颜色的单元格的最大数量：

dMax(orange) = dMin(orange) + U
dMax(red)    = dMin(red) + U
dMax(green)  = dMin(green) + U
dMax(yellow) = dMin(yellow) + U
dMax(blue)   = dMin(blue) + U

（在此特定示例中，U=0，因此每种颜色的最小单元数也是最大的）。

使用距离约束的寻路

如果我们要使用这些颜色约束强制枚举所有可能的组合，我们需要担心的组合就会少得多。更具体地说，在这个特定的示例中，我们将拥有：

  15! / (1! * 1! * 5! * 3! * 5!)
= 1307674368000 / 86400
= 15135120 combinations left, about a factor 2000 less.

但是，这仍然没有给我们实际的路径。所以一个更好的想法是回溯搜索，我们依次处理每种颜色并尝试找到所有路径：

  • 不穿过已经着色的单元格
  • 不短于 dMin（颜色）且不长于 dMax（颜色）。

第二个标准将减少每种颜色报告的路径数量，这导致尝试的路径总数大大减少（由于组合效应）。

在伪代码中：

function SolveLevel(initialBoard of size NxN)
{
    foreach(colour on initialBoard)
    {
        Find startCell(colour) and endCell(colour)
        minDistance(colour) = Length(ShortestPath(initialBoard, startCell(colour), endCell(colour)))
    }

    //Determine the number of uncoloured cells remaining after all shortest paths have been applied.
    U = N^(N^2 - 2N) - (Sum of all minDistances)

    firstColour = GetFirstColour(initialBoard)
    ExplorePathsForColour(
        initialBoard, 
        firstColour, 
        startCell(firstColour), 
        endCell(firstColour), 
        minDistance(firstColour), 
        U)
    }
}

function ExplorePathsForColour(board, colour, startCell, endCell, minDistance, nrOfUncolouredCells)
{
    maxDistance = minDistance + nrOfUncolouredCells
    paths = FindAllPaths(board, colour, startCell, endCell, minDistance, maxDistance)

    foreach(path in paths)
    {
        //Render all cells in 'path' on a copy of the board
        boardCopy = Copy(board)
        boardCopy = ApplyPath(boardCopy, path)

        uRemaining = nrOfUncolouredCells - (Length(path) - minDistance)

        //Recursively explore all paths for the next colour.
        nextColour = NextColour(board, colour)
        if(nextColour exists)
        {
            ExplorePathsForColour(
                boardCopy, 
                nextColour, 
                startCell(nextColour), 
                endCell(nextColour), 
                minDistance(nextColour), 
                uRemaining)
        }
        else
        {
            //No more colours remaining to draw
            if(uRemaining == 0)
            {
                //No more uncoloured cells remaining
                Report boardCopy as a result
            }
        }
    }
}

查找所有路径

这只留下 FindAllPaths(board, colour, startCell, endCell, minDistance, maxDistance) 被实现。这里的棘手之处在于我们不是在搜索最短路径，而是在由 minDistance 和 maxDistance 确定的范围内的任何路径。因此，我们不能只使用 Dijkstra 或 A*，因为它们只会记录到每个单元格的最短路径，而不是任何可能的弯路。

找到这些路径的一种方法是对电路板使用多维数组，其中每个单元格能够存储多个航路点，并且航路点被定义为一对（前一个航路点，到原点的距离）。一旦我们到达目的地，之前的航路点需要能够重建整个路径，并且到原点的距离防止我们超过 maxDistance。

然后可以通过从 startCell 向外使用类似洪水填充的探索来查找所有路径，其中对于给定的单元格，递归地探索每个未着色或与当前颜色相同的邻居（除了那些形成我们当前到原点的路径），直到我们到达 endCell 或超过 maxDistance。

该策略的一个改进是我们不从 startCell 向外探索到 endCell，而是从 startCell 和 endCell 向外并行探索，使用 Floor(maxDistance / 2) 和 Ceil(maxDistance / 2) 作为各自的最大距离。对于较大的 maxDistance 值，这应该将探索的单元数从 2 * maxDistance^2 减少到 maxDistance^2。

于 2012-10-24T09:36:44.130 回答
9

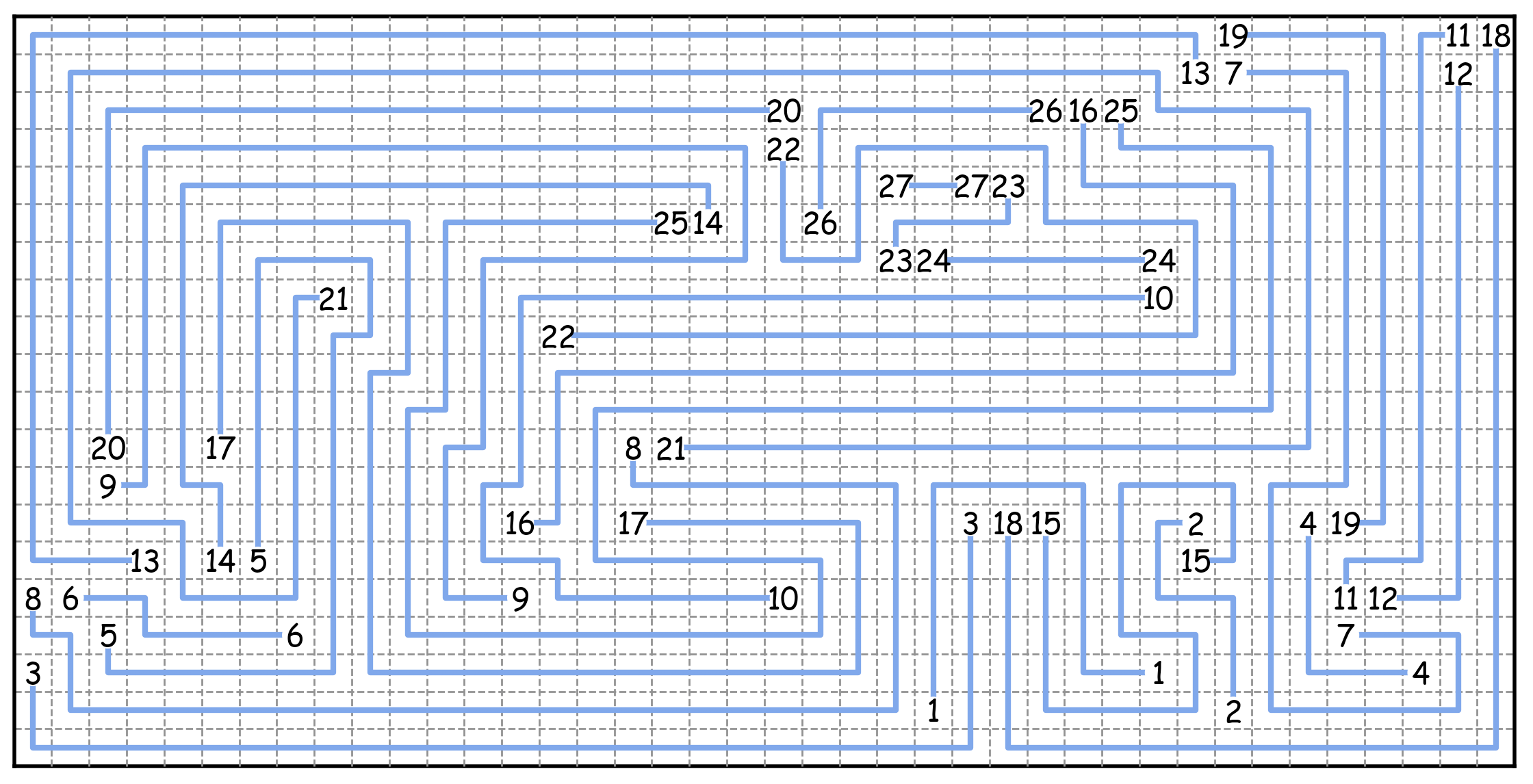
更新的答案：我使用“双重谜题”的想法实现了一个新的生成器。这比我知道的任何以前的方法都允许更稀疏和更高质量的谜题。代码在 github 上。我会尝试写更多关于它是如何工作的细节，但这里有一个示例拼图： 在此处输入链接描述

旧答案： 我在numberlink 求解器和生成器中实现了以下算法。In 强制执行规则，路径永远不能触及自身，这在大多数“硬核”数字链接应用程序和谜题中是正常的

  1. 首先，棋盘以简单、确定的方式用 2x1 多米诺骨牌平铺。如果这是不可能的（在奇数区域纸上），则右下角将保留为单例。
  2. 然后通过旋转随机的邻居对来随机打乱多米诺骨牌。在宽度或高度等于 1 的情况下不会这样做。
  3. 现在，在一张奇数区域纸的情况下，右下角连接到它的相邻多米诺骨牌之一。这将永远是可能的。
  4. 最后，我们可以开始寻找穿过多米诺骨牌的随机路径，并在我们通过时将它们组合起来。特别注意不要连接“邻居流”，这会产生“双重回归”的谜题。
  5. 在打印拼图之前，我们会尽可能“压缩”使用的颜色范围。
  6. 通过用 . 替换所有不是流头的位置来打印拼图。

我的 numberlink 格式使用 ascii 字符而不是数字。这是一个例子：

$ bin/numberlink --generate=35x20
Warning: Including non-standard characters in puzzle

35 20
....bcd.......efg...i......i......j
.kka........l....hm.n....n.o.......
.b...q..q...l..r.....h.....t..uvvu.
....w.....d.e..xx....m.yy..t.......
..z.w.A....A....r.s....BB.....p....
.D.........E.F..F.G...H.........IC.
.z.D...JKL.......g....G..N.j.......
P...a....L.QQ.RR...N....s.....S.T..
U........K......V...............T..
WW...X.......Z0..M.................
1....X...23..Z0..........M....44...
5.......Y..Y....6.........C.......p
5...P...2..3..6..VH.......O.S..99.I
........E.!!......o...."....O..$$.%
.U..&&..J.\\.(.)......8...*.......+
..1.......,..-...(/:.."...;;.%+....
..c<<.==........)./..8>>.*.?......@
.[..[....]........:..........?..^..
..._.._.f...,......-.`..`.7.^......
{{......].....|....|....7.......@..

在这里我通过我的求解器（相同的种子）运行它：

$ bin/numberlink --generate=35x20 | bin/numberlink --tubes
Found a solution!
┌──┐bcd───┐┌──efg┌─┐i──────i┌─────j
│kka│└───┐││l┌─┘│hm│n────n┌o│┌────┐
│b──┘q──q│││l│┌r└┐│└─h┌──┐│t││uvvu│
└──┐w┌───┘d└e││xx│└──m│yy││t││└──┘│
┌─z│w│A────A┌┘└─r│s───┘BB││┌┘└p┌─┐│
│D┐└┐│┌────E│F──F│G──┐H┐┌┘││┌──┘IC│
└z└D│││JKL┌─┘┌──┐g┌─┐└G││N│j│┌─┐└┐│
P──┐a││││L│QQ│RR└┐│N└──┘s││┌┘│S│T││
U─┐│┌┘││└K└─┐└─┐V││└─────┘││┌┘││T││
WW│││X││┌──┐│Z0││M│┌──────┘││┌┘└┐││
1┐│││X│││23││Z0│└┐││┌────M┌┘││44│││
5│││└┐││Y││Y│┌─┘6││││┌───┐C┌┘│┌─┘│p
5││└P│││2┘└3││6─┘VH│││┌─┐│O┘S┘│99└I
┌┘│┌─┘││E┐!!│└───┐o┘│││"│└─┐O─┘$$┌%
│U┘│&&│└J│\\│(┐)┐└──┘│8││┌*└┐┌───┘+
└─1└─┐└──┘,┐│-└┐│(/:┌┘"┘││;;│%+───┘
┌─c<<│==┌─┐││└┐│)│/││8>>│*┌?│┌───┐@
│[──[└─┐│]││└┐│└─┘:┘│└──┘┌┘┌┘?┌─^││
└─┐_──_│f││└,│└────-│`──`│7┘^─┘┌─┘│
{{└────┘]┘└──┘|────|└───7└─────┘@─┘

我已经测试了用迭代随机合并两条相邻路径的函数替换步骤 (4)。然而，它游戏的谜题要密集得多，我已经认为上面的内容几乎太密集了，很难。

这是我生成的不同大小的问题列表：https ://github.com/thomasahle/numberlink/blob/master/puzzles/inputs3

于 2012-12-22T23:54:06.643 回答
2

我认为您需要分两步执行此操作。步骤 1）找到一组连接所有点的非相交路径，然后 2）增长/移动这些路径以填充整个电路板

我对第 1 步的想法是基本上同时在所有点上执行类似 Dijkstra 的算法，使路径一起增长。与 Dijkstra 类似，我认为您会希望从每个点中填充填充，使用一些启发式方法选择下一个要搜索的节点（我的直觉是，首先选择自由度最小的点，然后是距离，可能是一个很好的）。与 Dijkstra 非常不同，尽管我认为当我们有多个路径试图增长到同一个节点时，我们可能会不得不回溯。（这在较大的地图上当然可能会有相当大的问题，但在像上面那样的小地图上可能不是什么大问题。）

在开始上述算法之前，您还可以解决一些更简单的路径，主要是为了减少所需的回溯次数。具体来说，如果您可以在棋盘边缘的点之间进行跟踪，则可以保证以这种方式连接这两个点不会干扰其他路径，因此您可以简单地填写它们并将这些人带出方程。然后，您可以进一步迭代，直到通过沿着板的边界或现有路径的边界跟踪找到所有这些“快速和简单”的路径。该算法实际上将完全解决上述示例板，但无疑会在其他地方失败.. 尽管如此，执行起来会非常便宜，并且会减少您对先前算法的搜索时间。

或者

您可以简单地在每组点之间执行真正的 Dijkstra 算法，首先找出最近的点（或以一些随机顺序尝试它们几次）。这可能适用于相当多的情况，当它失败时，只需扔掉地图并生成一个新地图。

一旦你解决了第 1 步，第 2 步应该会更容易，尽管不一定是微不足道的。为了发展你的路径，我认为你会想要向外扩展你的路径（所以首先是最靠近墙壁的路径，向墙壁生长，然后是向外的其他内部路径，等等）。要成长，我认为你将有两个基本操作，翻转角落，并扩展到相邻的空方块对..也就是说，如果你有一条线

.v<<.
v<...
v....
v....

首先，您需要翻转角落以填充边缘空间

v<<<.
v....
v....
v....

然后你会想要扩展到相邻的开放空间对

v<<v.
v.^<.
v....
v....

v<<v.
>v^<.
v<...
v....

ETC..

请注意，如果存在解决方案，我所概述的内容不能保证解决方案，但我认为如果存在解决方案，您应该能够在大多数情况下找到解决方案，然后在地图没有解决方案或算法无法解决的情况下找到一张，扔掉地图，换一张试试：）

于 2012-10-17T04:03:09.363 回答
1

你有两个选择：

  1. 编写自定义求解器
  2. 蛮力它。

我使用选项 (2) 来生成 Boggle 类型的板，并且非常成功。如果您选择选项 (2)，您可以这样做：

所需工具：

  • 编写一个 A* 求解器。
  • 写一个随机板创建者

要解决：

  1. 生成仅包含端点的随机棋盘
  2. 虽然板子没有解决：
    • 获得两个彼此最近但尚未解决的端点
    • 运行 A* 生成路径
    • 更新电路板，以便下一个 A* 知道新电路板布局，新路径标记为不可遍历。
  3. 在循环退出时，检查成功/失败（是否使用了整个板/等）并在需要时再次运行

10x10 上的 A* 应该在百分之一秒内运行。您可能可以解决 1k+ 板/秒。所以 10 秒的运行应该让你得到几个“可用”的板。

奖励积分：

  • 在为 IAP（应用内购买）关卡包生成关卡时，请记住检查镜像/旋转/反射/等，这样您就没有一个板与另一个板的副本（这只是蹩脚）。
  • 提出一个衡量标准，以确定两个板是否“相似”，如果是，则放弃其中一个。
于 2014-02-10T14:09:47.027 回答