1

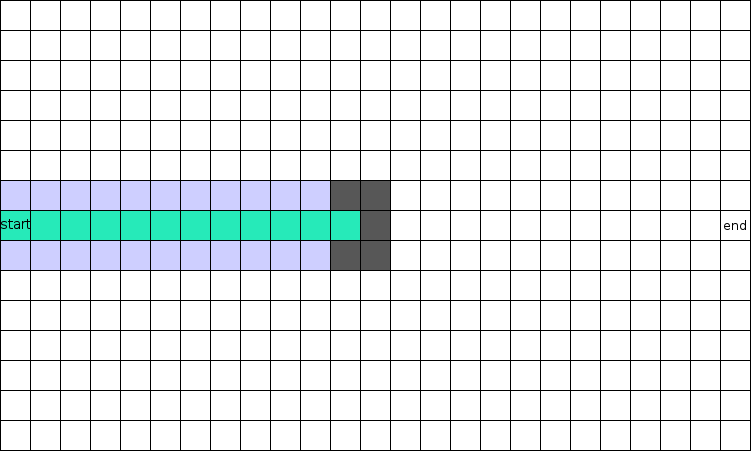
我正在编写一个塔防游戏，并且我正在实现教程中的 A* 寻路算法等等，但是我遇到了一个我无法编写代码的情况！考虑下图。青色节点代表目前发现的最短路径，紫色节点代表已检查节点，深灰色节点代表一堵墙。

根据我对 A* 算法的了解，要计算以下情况的路径，它...

  1. 从“start”开始并检查上层节点是否可用。这是。它计算其 G 和 H 分数。它对右、下和左节点执行相同的操作。
  2. 发现右节点的 F 分数最低 (F = G + H)。然后它重复与步骤 #1 相同的方法来查找下一个节点，将“开始”节点标记为父节点。
  3. 继续这种模式并落在“C 陷阱”中心的节点上，因为该节点迄今为止的 F 分数最低。
  4. 发现上、右、下、左节点全部闭合。A* 然后将该节点标记为已关闭并重新开始，理解不要理会该节点。

#4 之后会发生什么？ A* 会沿着同一条路径重新检查 G 和 H 分数，跳过那个新关闭的节点吗？此外，当使用此 SWF绘制此场景时，表明发现了更多节点来弥补陷阱，如此处建议的那样。为什么？

A* 问题的图形

4

1 回答 1

1

您似乎缺少的是，A* 不像单个单元沿着网格移动，并且在撞到墙壁时会回溯；它更像是一个观察者在查看图表周围的各个节点，总是考虑下一个“最有可能”在最短路径中的节点。

所以，上面的第 4 步永远不会发生。当 A* 确定它不能成为最佳路径的一部分时，它不会将节点标记为已关闭 - 它只是将它访问的每个节点放在closed列表中，只要它访问它。而且它永远不会“重新开始”——它总是查看下一个“最有可能”的节点，其中“最有可能”是指按 .排序的优先级队列f(x)的前面。

因此，在上面的示例中，A* 接下来将跳转到其中一个蓝色节点，因为它们都在open列表中，并且都具有相同的f(x)值。虽然它可以在技术上考虑接下来的任何一个，但如果您使用正确的打破平局标准，它将采用最接近结束的两个之一。

于 2012-10-03T12:23:05.693 回答