假设一个游戏中一个人掷出 20 个 8 面骰子,总共有 8^20 种可能的结果。为了计算特定事件发生的概率,我们将事件发生的方式数除以 8^20。
可以计算出正确获得 5 个骰子值 3 的方法的数量。(20 选择 5)给了我们 3 的订单数量。7^15 给了我们在 15 次掷骰中无法获得 3 的方式的数量.
number of ways to get exactly 5, 3's = (20 choose 5)*7^15.
答案也可以看成我可以用多少种方式重新排列字符串 3,3,3,3,3,0,0,0,0,0,0,0,0,0,0,0,0,0 ,0,0(20 选择 5)乘以我们为零的值的总数(假设 7 个合法值)7^15(这是正确的)。
问题 1:我如何计算获得完全相同值的 5 个骰子的方法数量(即,对于所有骰子值)。注意:如果我只是天真地使用上面的第一个答案并乘以 bt 8,我会得到大量的重复计算吗?
我知道我可以解决每种情况 (5 1's), (5, 2's), (5, 3's), ... (5's, 8) 对它们求和(更简单地说 8*(5 1's) )。然后减去重叠数的总和 (5 1's) 和 (5 2's), (5 1's) 和 (5 3's)... (5 1's) 和 (5, 2's) 和 ...和 (5, 8's)但这似乎非常混乱。我会以一种扩展到大量样本和大量类的方式对此进行概括。
如何计算获得至少5 个相同值的骰子的方法数?
所以 111110000000000000000 或 11110100000000000002 或 11111100000001110000 或 11011211222222223333,但不是 00001111222233334444 或 0630511514225。
我正在寻找解释数学或指向支持此的库(尤其是 python 模块)的答案。细节和例子的加分。
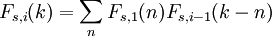
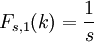 为0。
为0。